用长L=0.5米的细绳,一端拴一质量m=1千克的小球,另一端固定在离水平桌高h=O.3米的O点上,使小球在光滑桌面上做匀速圆周运动(如图所示)。
(1)如果运动速率v=1.2米/秒,求此时绳对球的拉力与球对桌面的压力;
(2)为使小球不离开桌面做圆周运动,它的速率不能超过多大?
跳伞运动员做低空跳伞表演,他离开飞机后先做自由落体运动,当距离地面 125 m时打开降落伞,伞张开后运动员就以大小为14.3 m/s2的加速度做匀减速运动,到达地面时速度为5 m/s,问:(1)运动员离开飞机时距地面的高度为多少?(2)离开飞机后,经过多少时间才能到达地面?(g="10" m/s2)
(9分)如图,A与B两滑块叠放在水平面上,已知A与B的重力分别为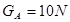 ,
,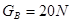 ,A与B间的动摩擦因素
,A与B间的动摩擦因素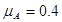 ,B与水平面间的动摩擦因素
,B与水平面间的动摩擦因素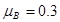 。在用水平拉力F把B向左匀速拉出的过程中,
。在用水平拉力F把B向左匀速拉出的过程中,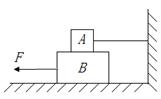
求:(1)地面对B的摩擦力大小。
(2)拉力F的大小。
(9分)某种类型的飞机起飞滑行时,从静止开始做匀加速运动,加速度大小为4.0m/s2,飞机速度达到85m/s时离开地面升空.如果在飞机达到起飞速度时,突然接到命令停止起飞,飞行员立即使飞机制动,飞机做匀减速运动,加速度大小为5.0m/s2.如果要求你为该类型的飞机设计一条跑道,使在这种情况下飞机停止起飞而不滑出跑道,你设计的跑道长度至少要多长?
一列货车以6m/s的速度在平直铁路上运动,由于调度失误,在它后面120m处有一列客车20m/s的速度向它靠近,客车司机发觉后立即合上制动器,客车以1m/s2的加速度做匀减速运动,试判断两车是否会相撞?若不相撞试求出二者之间的最小距离;若相撞求出相撞时客车的速度
如图所示,长L = 35cm的铁链,上端用一很短的细线悬挂,距铁链下端h = 45cm处有一A点。现剪断细线,让铁链自由下落,不计空气阻力,取g = 10m/s2。
求:(1)铁链下端经过A点时的速度大小υ;
(2)整条铁链通过A点所用的时间△t。