已知数列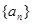 满足如图所示的程序框图.
满足如图所示的程序框图.
(Ⅰ) 写出当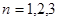 时输出的结果;
时输出的结果;
(Ⅱ) 写出数列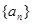 的一个递推关系式,并证明:
的一个递推关系式,并证明: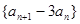 是等比数列;
是等比数列;
(Ⅲ)求 的通项公式及前
的通项公式及前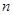 项和
项和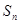 .
.
如图所示,已知三棱柱ABC A1B1C1,
A1B1C1,
(1)若M、N分别是AB,A1C的中点,求证:MN∥平面BCC1B1;
(2)若三棱柱ABC A1B1C1的各棱长均为2,∠B1BA=∠B1BC=60°,P为线段B1B上的动点,当PA+PC最小时,求证:B1B⊥平面APC.
A1B1C1的各棱长均为2,∠B1BA=∠B1BC=60°,P为线段B1B上的动点,当PA+PC最小时,求证:B1B⊥平面APC.
如图所示,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF⊥平面EFDC,设AD中点为P.
(1)当E为BC中点时,求证:CP∥平面ABEF;
(2)设BE=x,问当x为何值时,三棱锥A CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.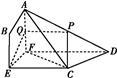
一个多面体的直观图和三视图如图所示,其中M,N分别是AB,AC的中点,G是DF上的一动点.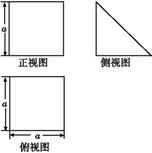
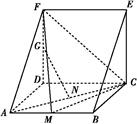
(1)求该多面体的体积与表面积;
(2)求证:GN⊥AC;
(3)当FG=GD时,在棱AD上确定一点P,使得GP∥平面FMC,并给出证明.
如图所示,四棱锥E ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.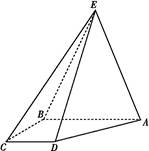
(1)求证:AB⊥ED;
(2)线段EA上是否存在点F,使DF∥平面BCE?若存在,求出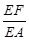 ;若不存在,说明理由.
;若不存在,说明理由.
如图五面体中,四边形ABCD是矩形,DA⊥平面ABEF,AB∥EF,AB=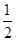 EF=2
EF=2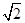 ,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.
,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.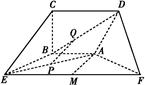
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面ADF.