太阳内部持续不断地发生着 4 个质子聚变为一个氦核的热核反应,这个核反应释放出的大量能量就是太阳的能源。求:
(1)写出这个核反应方程。
(2)这一核反应能释放多少能量?
(3)已知太阳每秒释放的能量为 3.8 ×1026,则太阳每秒减少的质量为多少kg?( 为正电子符号,质子质量 mp ="1.0073" u,α粒子质量 m =" 4.0015" u,电子质量 me =" 0.00055" u,1 u 质量相当于 931.5 MeV 能量)
为正电子符号,质子质量 mp ="1.0073" u,α粒子质量 m =" 4.0015" u,电子质量 me =" 0.00055" u,1 u 质量相当于 931.5 MeV 能量)
在心电图仪、地震仪等仪器工作过程中,要进行振动记录,如图甲所示是一个常用的记录方法,在弹簧振子的小球上安装一支记录用笔P,在下面放一条白纸带.当小球振动时,匀速拉动纸带(纸带运动方向与振子振动方向垂直),笔就在纸带上画出一条曲线,如图乙所示.
(1)若匀速拉动纸带的速度为1 m/s,则由图中数据算出振子的振动周期为多少?
(2)作出P的振动图象.
(3)若拉动纸带做匀加速运动,且振子振动周期与原来相同,由图丙中的数据求纸带的加速度大小.
“嫦娥二号”载人飞船的成功发射,标志着我国航天技术新的突破.如果宇航员将在地面上校准的摆钟拿到月球上去.
(1)若此钟在月球上记录的时间是1 h,那么实际的时间是多少?
(2)若要在月球上使该钟与在地面上时一样准,摆长应如何调节?(已知g月=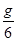 )
)
如图甲是一个单摆振动的情形,O是它的平衡位置,B、C是摆球所能到达的最远位置.设摆球向右运动为正方向.图乙是这个单摆的振动图象.根据图象回答: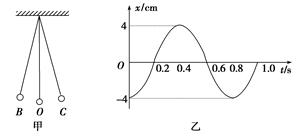
(1)单摆振动的频率是多大?
(2)开始时刻摆球在何位置?
(3)若当地的重力加速度为10 m/s2,这个摆的摆长是多少?
电压u=120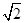 sinωt V,频率为50 Hz的交变电流,把它加在激发电压和熄灭电压均为u0=60
sinωt V,频率为50 Hz的交变电流,把它加在激发电压和熄灭电压均为u0=60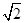 V的霓虹灯的两端.
V的霓虹灯的两端.
(1)求在一个小时内,霓虹灯发光时间有多长?
(2)试分析为什么人眼不能感到这种忽明忽暗的现象?(已知人眼的视觉暂留时间约为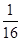 s)
s)
如图所示,间距为L的光滑水平金属导轨,水平地放置在竖直方向的磁感应强度为B的匀强磁场中,一端接阻值为R的电阻.质量为m的导体棒放置在导轨上,其电阻为R0.在拉力F作用下从t=0的时刻开始运动,其速度随时间的变化规律为v=vmsinωt,不计导轨电阻.求: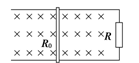
(1)从t=0到t=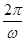 时间内电阻R产生的热量.
时间内电阻R产生的热量.
(2)从t=0到t=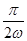 时间内拉力F所做的功.
时间内拉力F所做的功.