有同学这样探究太阳的密度:正午时分让太阳光垂直照射一个当中有小孔的黑纸板,接收屏上出现一个小圆斑;测量小圆斑的直径和黑纸板到接收屏的距离,可大致推出太阳直径。他掌握的数据是:太阳光传到地球所需的时间、地球的公转周期、万有引力恒量;在最终得出太阳密度的过程中,他用到的物理规律是小孔成像规律和 ( )
| A.牛顿第二定律 | B.万有引力定律 |
| C.万有引力定律、牛顿第二定律 | D.万有引力定律、牛顿第三定律 |
如图甲所示,矩形金属线框绕与磁感线垂直的转轴在匀强磁场中匀速转动,输出交变电流的电动势图象如图乙所示,经原、副线圈匝数比为1:10的理想变压器给一灯泡供电,如图丙所示,副线圈电路中灯泡的额定功率为22W,现闭合开关,灯泡正常发光.则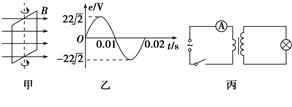
| A.t=0.01s时,穿过线框回路的磁通量为零 |
| B.金属线框的转速为50r/s |
C.变压器原线圈中电流表的示数为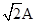 |
| D.灯泡的额定电压为220V |
在如图甲所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2.螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF.在一段时间内,穿过螺线管的磁场的磁感应强度B按如图乙所示的规律变化.则下列说法中正确的是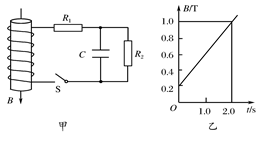
| A.螺线管中产生的感应电动势为1.2V |
| B.闭合S,电路中的电流稳定后电容器上极板带正电 |
| C.电路中的电流稳定后,电阻R1的电功率为5×10-2W |
| D.S断开后,流经R2的电量为1.8×10-5C |
如图所示,在光滑绝缘水平面上的P点正上方O点固定了一电荷量为+Q的正点电荷,在水平面上的N点,由静止释放一质量为m、电荷量为-q的负检验电荷,该检验电荷经过P点时速度为v,图中θ=60°,规定电场中P点的电势为零,则在+Q形成的电场中,下列判断正确的是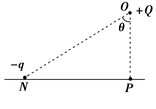
| A.P点电场强度大小是N点的2倍 |
| B.N点电势高于P点电势 |
C.N点电势为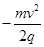 |
D.检验电荷在N点具有的电势能为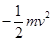 |
如图甲所示,一轻杆一端固定在O点,另一端固定一小球,在竖直平面内做半径为R的圆周运动.小球运动到最高点时,杆与小球间弹力大小为FN,小球在最高点的速度大小为v,FN-v2图象如图乙所示.下列说法正确的是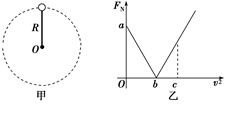
A.当地的重力加速度大小为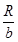 |
B.小球的质量为 |
| C.当v2=c时,杆对小球弹力方向向上 |
| D.若v2=2b,则杆对小球弹力大小为2a |
火星的直径为地球的一半,质量为地球的十分之一,它绕太阳公转的轨道半径约为地球绕太阳公转的轨道半径的1.5倍,地球表面重力加速度约为10m/s2,从以上信息可知
| A.火星公转的周期比地球公转的周期短 |
| B.火星表面重力加速度约为4m/s2 |
| C.火星公转的向心加速度比地球公转的向心加速度大 |
| D.火星公转的线速度大于地球公转的线速度 |