如图15所示，平行金属导轨与水平面间夹角均为θ= 370 ，导轨间距为 lm ，电阻不计，导轨足够长。两根金属棒 ab 和 a’b’的质量都是0.2kg，电阻都是 1Ω ，与导轨垂直放置且接触良好，金属棒a’b’和导轨之间的动摩擦因数为0.5 ，金属棒ab和导轨无摩擦，导轨平面PMKO处存在着垂直轨道平面向上的匀强磁场，导轨平面PMNQ处存在着沿轨道平面向上的匀强磁场，磁感应强度 B 的大小相同．让a’ b’固定不动，将金属棒ab 由静止释放，当 ab 下滑速度达到稳定时，整个回路下滑速度达到稳定时，整个回路消耗的电功率为 18W 。求 ：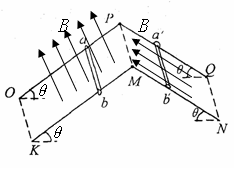
( 1 ) ab 达到的最大速度多大？
( 2) ab 下落了 30m 高度时，其下滑速度已经达到稳定，则此过程中回路电流的发热量 Q 多大？
( 3) 在ab下滑过程中某时刻将 a ' b’固定解除，为确保a ' b’始终保持静止，则a ' b’固定解除时ab棒的速度有何要求？ ( g ="10m" / s2 , sin370 ="0.6" ,cos370 ="0.8" )
在光滑的水平面上有一直角坐标．质量为m＝4 kg的物体，沿y轴正方向以大小为5 m/s的初速度通过坐标原点O，此时给物体施加一沿x轴正方向的恒力F。一段时间后物体恰好通过点P，P点的坐标为（2.5 m，5 m）。求：
（1）物体由O运动到P点的时间；
（2）恒力F的大小；
（3）物体在P点的速度的大小和方向
我国北方冬季需要对房间空气加热，设有一房面积为14m2，高为3m，室内空气通过房间缝隙与外界大气相通，开始时室内空气温度为10℃，通过加热变为20℃
（1）已知空气的摩尔质量为29g/mol，标准状况下1mol气体的体积为22．4L，阿伏加德罗常数为NA=6．02×1
023mol-1，试计算这个过程中有多少个空气分子从室内跑出。（结果保留2位有效数字）
（2）已知气体热运动的平均动能跟热力学温度成正比，即Ek=kT，空气可以看作理想气体，试通过分析、计算说明室内空气的内能随温度的升降如何变化
如图所示，直线MN与水平线夹角为60°，其右侧有一垂直纸面向外的范围足够大的匀强磁场，磁感应强度为Ｂ；直线ＰＱ垂直ＭＮ，且ＰＱ与ＭＮ包围的空间有一匀强电场，电场方向平行于ＰＱ。有一质量为m 电量为+q的带电粒子在纸面内以v0的水平初速度从A点飞入磁场，粒子进入磁场t0（t0未知）时间后立即撤除磁场，此时粒子未到达MN，之后粒子垂直MQ边界从C点（图中未画出）飞入电场；随后粒子再次通过C点。粒子在以上整个过程中所用总时间恰为此带电粒子在磁场中运动一周所需时间，粒子所受重力不计。试求：
（1）粒子在磁场中运动的时间t0
（2）匀强电场场强E的大小。
物块A（可以看成质点）静止在一斜面的底端，斜面倾角a ＝30°，斜面的长为L=1m，物块A与斜面之间的滑动摩擦因数
，斜面固定在水平桌面上。用轻绳跨过斜面顶端的轻滑轮与物块A连接，滑轮与转轴之间的摩擦不计，开始绳刚好绷直，如图所示。若在绳的末端施一竖直向下的恒力F=12N拉绳，物块A由斜面底端到顶端经历的时间为1s。取重力加速度g=10m/s2
（1）物块A的质量mA是多大？
（2）若物块A静止在斜面底端时，在绳的末端绕过定滑轮挂一质量为1．5kg的物块B由手托住（图中没画出），开始时绳也刚好绷直，则由静止松手后物块A从斜面底端到顶端时B的动能为多少？
（1）下列说法正确的是：
| A．实际上，原子中的电子没有确定的轨道，但在空间各处出现的概率具有一定的规律 |
| B．核力是短程力，且总表现为吸引力，从而使核子结合在一起 |
| C．太阳辐射能量主要来源于重核裂变 |
| D．各种原子的发射光谱都是线状谱 |
（2）一炮弹质量为m，以一定的倾角斜向上发射。到达最高点时速度为v，炮弹在最高点爆炸成两块。其中一块沿原轨道返回，质量为m/2，求爆炸过程中系统增加的机械能。