如图所示,一等腰直角棱镜,放在真空中,AB=AC=d.在棱镜侧面AB左方有一单色光源S,从S发出的光线SD以60°入射角从AB侧面中点射入,当它从侧面AC射出时,出射光线偏离入射光线的偏向角为30°,若测得此光线传播的光从光源到棱镜面AB的时间跟在棱镜中传播的时间相等,那么点光源S到棱镜AB侧面的垂直距离是多少?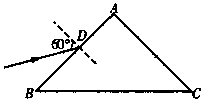
如图所示,两平行金属板P1和P2之间的电压为U。一个带负电的粒子在两板间沿虚线所示路径做加速直线运动。 粒子通过两平行板后从O点进入另一磁感应强度为B的匀强磁场中,在洛伦兹力的作用下,粒子做匀速圆周运动,经过半个圆周后打在挡板MN上的A点。 已知粒子的质量为m,电荷量为q。 不计粒子重力。 求:
(1)粒子进入磁场时的速度v;
(2)O、A两点间的距离x。
在与水平面成60°角的光滑金属导轨间连一电源,在相距为1m的平行导轨上放一质量为0.3kg的金属棒ab,通以3A的由b向a的电流,磁场方向竖直向上,这时棒恰好静止.
求:(1)磁感应强度B
(2)棒对导轨的压力大小.(g取10m/s2)
一台电风扇,内阻为10Ω,接上220V的电压后正常运转,此时它消耗的电功率是66W,求:
(1)通过电动机的电流是多少?
(2)该电风扇转化为机械能的功率是多少?
(3)如接上220V电源后,扇叶被卡住不能转动(没有被烧坏前),该电风扇消耗的电功率是多少?
如图所示,匀强磁场的磁感强度B=0.20T,方向沿x轴正方向,且ab=40cm,bc=30cm,ac=50cm,且abc所在平面与xOz平面平行,分别求出通过面积abod、bofc、acfd的磁通量 、
、 、
、

在如图所示的空间区域里,y轴左方有一匀强电场,场强方向跟y轴负方向成30°角,大小为E = 4.0×105N/C,y轴右方有一垂直纸面的匀强磁场,有一质子以速度υ0 = 2.0×106m/s由x轴上A点(OA =" 10" cm)先后两次进入磁场,第一次沿x轴正方向射入磁场,第二次沿x轴负方向射入磁场,回旋后都垂直射入电场,最后又进入磁场,已知质子质量m为1.6×10-27kg,不计质子重力,求: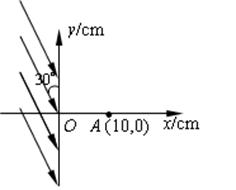
(1)匀强磁场的磁感应强度大小和方向;
(2)质子两次在磁场中运动的时间之比;
(3)质子两次在电场中运动的时间各为多少?