弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,B、C相距20cm..t=0时刻振子处于B点,经过0.5s,振子首次到达C点,求:
(1) 振子在5s内通过的路程及5秒末位移大小
(2)振子在B点的加速度大小跟它距O点4cm处P点的加速度大小的比值
如图所示,在粗糙水平台阶上静止放置一质量m=0.5kg的小物块,它与水平台阶表面的动摩擦因数μ=0.5,且与台阶边缘O点的距离s=5m.在台阶右侧固定了一个1/4圆弧挡板,圆弧半径R=1m,圆弧的圆心也在O点。今以O点为原点建立平面直角坐标系.现用F=5N的水平恒力拉动小物块,一段时间后撤去拉力,小物块最终水平抛出并击中挡板.(g取10m/s 2 )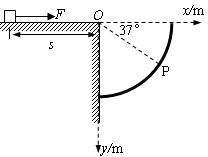
(1)若小物块恰能击中档板上的P点(OP与水平方向夹角为37°,已知sin37°=0.6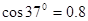 ,则其离开O点时的速度大小;
,则其离开O点时的速度大小;
(2)为使小物块击中档板,求拉力F作用的最短时间;
(3)改变拉力F的作用时间,使小物块击中挡板的不同位置.求击中挡板时小物块动能的最小值.
下图是某传送装置的示意图。其中PQ为水平的传送带,传送带长度L=6m。MN是光滑的曲面,曲面与传送带相切于N点。现在有一滑块质量为m=3kg从离N点高为h="5m" M处静止释放,滑块与传送带间的摩擦系数为μ=0.3。重力加速度为g="10m/s" 2 。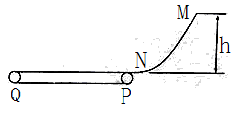
(1)滑块以多大的速度进入传送带?
(2)若传送带顺时针转动,滑块以多大的速度离开传送带?
(3)若传送带顺时针转动且速度大小为v,求出滑块与传送带摩擦产生的热量Q与传送带的速度v的大小关系。
下暴雨时,有时会发生山体滑坡或泥石流等地质灾害。某地有一倾角为θ=37°(sin37°="0.6" 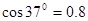 )的山坡C,上面有一质量为2m的石板B,其上下表面与斜坡平行;B上有一碎石堆A(含有大量泥土),A和B均处于静止状态,如图所示。假设某次暴雨中,A浸透雨水后总质量为m(可视为质量不变的滑块),在极短时间内,A、B间的动摩擦因数μ1减小为
)的山坡C,上面有一质量为2m的石板B,其上下表面与斜坡平行;B上有一碎石堆A(含有大量泥土),A和B均处于静止状态,如图所示。假设某次暴雨中,A浸透雨水后总质量为m(可视为质量不变的滑块),在极短时间内,A、B间的动摩擦因数μ1减小为 ,B、C间的动摩擦因数μ2减小为0.5,A、B开始运动。已知A开始运动时,A离B下边缘的距离l=12m,C足够长。取重力加速度大小g=10m/s2。求:
,B、C间的动摩擦因数μ2减小为0.5,A、B开始运动。已知A开始运动时,A离B下边缘的距离l=12m,C足够长。取重力加速度大小g=10m/s2。求: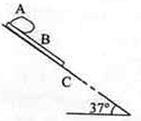
(1)A和B加速度的大小;
(2)A在B上运动的时间
某星球的质量约为地球质量的8倍,半径约为地球半径的2倍。已知地球的第一宇宙速度为7.9 km/s,则航天器在该星球表面附近绕星球做匀速圆周运动的速度大小约为多少?
交管部门为了监测汽车是否按规定的限速行驶,以保安全,在我们学校校门前安装了电子测速仪,来检查是否超过40km/h的限速。其工作原来是:测速仪先后两次发出并接受超声波信号,再根据两次信号的时间差,测出被测车辆的速度。如果某次检测车速时,第一次从发出至接受到超声波信号用了0.4秒,第二次从发出至接收到超声波信号用了0.3秒,两次信号发出的时间间隔是1秒,则被测汽车的速度是多少?是否超速?(假设超声波速度 =340米/秒,且保持不变;发射和接受的声波信号脉冲如监视屏上所示)
=340米/秒,且保持不变;发射和接受的声波信号脉冲如监视屏上所示)

(提示:规范答题和形成良好的解题思路是我们解决物理问题必须具备的良好习惯,对于14题按指定的思路先进行分析,然后规范答题)