如图所示,质量为m的小球自由下落d后,沿竖直面内的固定轨道ABC运动,AB是半径为d的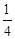 光滑圆弧,BC是直径为d的粗糙半圆弧(B是轨道的最低点)。小球恰好能运动到C点.求:
光滑圆弧,BC是直径为d的粗糙半圆弧(B是轨道的最低点)。小球恰好能运动到C点.求:
(1)小球运动到B处时对轨道的压力大小;
(2)小球在BC上运动过程中,摩擦力对小球做的功。(重力加速度为g)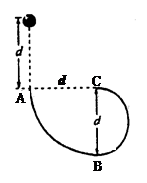
如图所示,甲为某一波在t=0时的图象,乙为参与该波动的P质点的振动图象.
(1)试确定波的传播方向;
(2)求该波的波速v;
(3) 求再经过3.5 s时P质点的路程s和位移.
如图所示,两足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直.一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定为I.整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.求:
(1)磁感应强度的大小B;
(2)电流稳定后,导体棒运动速度的大小v;
(3)流经电流表电流的最大值Im.
如图所示,质量为m=0.5kg的物体放在质量为M=4.5kg的平台上,随平台上、下做简谐运动.设在简谐运动过程中,二者始终保持相对静止.已知弹簧的劲度系数为k=400N/m,振幅为A=0.1m.。试求:二者一起运动到最低点时,物体对平台的压力大小;(取g=10m/s)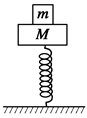
如图所示,长度为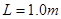 的绳,拴着一质量
的绳,拴着一质量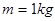 的小球在竖直面内做圆周运动,小球半径不计,已知绳子能够承受的最大张力为19N,圆心离地面高度
的小球在竖直面内做圆周运动,小球半径不计,已知绳子能够承受的最大张力为19N,圆心离地面高度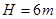 ,运动过程中绳子始终处于绷紧状态求:
,运动过程中绳子始终处于绷紧状态求:
(1)分析绳子在何处最易断,求出绳子断时小球的线速度;
(2)绳子断后小球落地点与抛出点的水平距离多大?落地时速度多大? 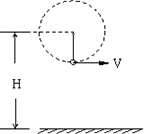
2008年9月25日,我国继“神舟”五号、六号载人飞船后又成功地发射了“神舟”七号载人飞船。如果把“神舟”七号载人飞船绕地球运行看作是同一轨道上的匀速圆周运动,宇航员测得自己绕地心做匀速圆周运动的周期为T、距地面的高度为H,且已知地球半径为R、地球表面重力加速度为g,万有引力恒量为G。你能计算出下面哪些物理量?能计算的量写出计算过程和结果,不能计算的量说明理由。
(1)地球的质量 ;
(2)飞船线速度的大小;
(3)飞船所需的向心力。