质点做匀速圆周运动时,下面物理量中不变的是:
| A.线速率 | B.线速度 | C.加速度 | D.角速度 |
一辆汽车4s内作匀加速直线运动,初速度为2m/s,末速度为10m/s,在这段时间内()
| A.汽车的加速度为2m/s2 |
| B.汽车的加速度为8m/s2 |
| C.汽车的平均速度为6m/s |
| D.汽车的加速度为10 m/s2 |
下图中,表示物体不是做匀速直线运动的图象是()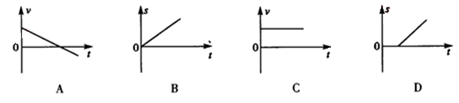
用如图所示的四种方法悬挂一个镜框,绳中所受拉力最小的是:()
如右图所示,杯子落到水平桌面时,则下列说法正确的是:( )
| A.力F1就是杯子的重力 |
| B.力F1和力F2是一对平衡力 |
| C.力F1和力F2是一对作用力和反作用力 |
| D.力F1的大小大于力F2的大小 |

自然界存在着四种基本相互作用,万有引力、电磁力、强相互作用和弱相互作用。它们是不需要物体相互接触就能起作用的。下列选项正确的是
| A.弹力和摩擦力是接触力,因此不属于四种基本相互作用 |
| B.弹力和摩擦力虽然是接触力,但它们在本质上都是由电磁力引起的 |
| C.强相互作用的作用范围很小,因此弹力等接触力属于强相互作用 |
| D.弱相互作用就是作用力很小的力 |