点A(-3,2)向左平移2个单位长度后得到的点的坐标为( ).
| A.(-3,0) | B.(-1,0) | C.(-1,2) | D.(-5,2) |
下列运算正确的是( ).
A.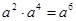 |
B. |
C. |
D.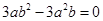 |
下列各式,正确的是( ).
| A.-2﹥1 | B.-3 ﹥-2 | C.   |
D. |
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下次沿顺时针方向跳两个点;若停在偶数点上,则下次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经过2012次后它停在哪个数对应的点上()
| A.1 | B.2 | C.3 | D.5 |

如图,在 中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是()
中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是()
| A.4.8 | B.4.75 | C.5 | D. |

在数-1,1,2中任取两个数作为点坐标,那么该点刚好在一次函数 图象上的概率是()
图象上的概率是()
A. 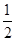 |
B.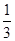 |
C.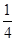 |
D.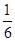 |