在研究勾股定理时,同学们都见到过图1,∠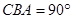 ,四边形
,四边形 、
、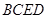 、
、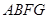 都是正方形.
都是正方形.
⑴连结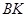 、
、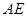 得到图2,则△
得到图2,则△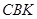 ≌△
≌△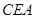 ,此时两个三角形全等的判定依据是
,此时两个三角形全等的判定依据是
▲ ;过 作
作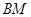 ⊥
⊥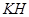 于
于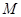 ,交
,交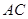 于
于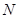 ,则
,则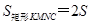 △
△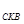 ;同理
;同理 △
△ ,得
,得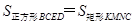 ,然后可证得勾股定理.
,然后可证得勾股定理.
⑵在图1中,若将三个正方形“退化”为正三角形,得到图3,同学们可以探究△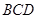 、△
、△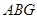 、△
、△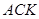 的面积关系是 ▲ .
的面积关系是 ▲ .
⑶为了研究问题的需要,将图1中的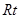 △
△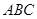 也进行“退化”为锐角△
也进行“退化”为锐角△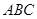 ,并擦去正方形
,并擦去正方形 得图4,由
得图4,由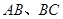 两边向三角形外作正△
两边向三角形外作正△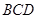 、正△
、正△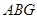 ,△
,△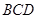 的外接圆与
的外接圆与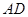 交于点
交于点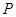 ,此时
,此时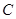 、
、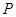 、
、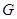 共线,从△
共线,从△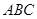 内一点到
内一点到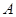 、
、 、
、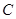 三个顶点的距离之和最小的点恰为点
三个顶点的距离之和最小的点恰为点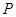 (已经被他人证明).设
(已经被他人证明).设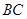 =3,
=3,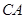 =4,
=4,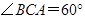 .求
.求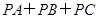 的值.
的值.
如图,已知二次函数L1:y=ax2-2ax+a+3(a>0)和二次函数L2:y=-a(x+1)2+1(a>0)图像的顶点分别为M,N,与y轴分别交于点E,F.
(1)函数y=ax2-2ax+a+3(a>0)的最小值为;当二次函数L1,L2的y值同时随着x的增大而减小时,x的取值范围是;
(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明);
(3)若二次函数L2的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程-a(x+1)2+1=0的解.
甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别在A,B两端同时出发,分别到另一端点掉头,掉头时间不计,速度分别为5m/s和4m/s.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);
(2)根据(1)中所画图象,完成下列表格:
| 两人相遇次数 (单位:次) |
1 |
2 |
3 |
4 |
… |
n |
| 两人所跑路程之和(单位:m) |
100 |
300 |
… |
(3)①直接写出甲、乙两人分别在第一个100m内,s与t的函数解析式,并指出自变量t的取值范围;
②求甲、乙第6此相遇时t的值.
如图,已知直线y=ax+b与双曲线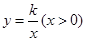 交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于点P(x0,0),与y轴交于点C.
交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于点P(x0,0),与y轴交于点C.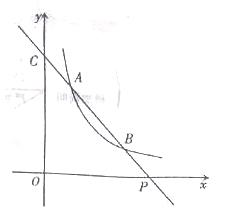
(1)若A,B两点坐标分别为(1,3),(3,y2).求点P的坐标;
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标;
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
(1)如图1,纸片□ABCD中,AD=5,S□ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为()
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图2,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.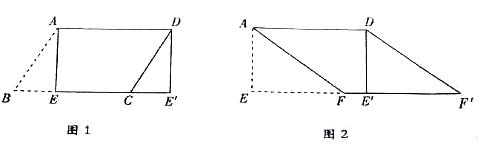
某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生的家长1份,每份问卷仅表明一种态度.将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如下两幅不完整的统计图.
学生家长对孩子使用手机的态度情况统计图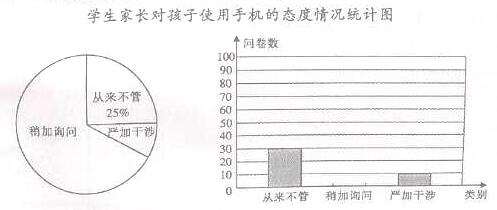
根据以上信息回答下列问题:
(1)回收的问卷数为份,“严加干涉”部分对应扇形的圆心角度数为;
(2)把条形统计图补充完整;
(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?