若一个角的余角是它的补角的 ,求这个角的度数.
,求这个角的度数.
如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).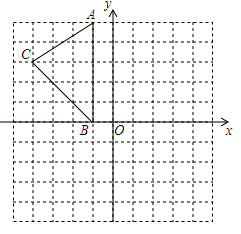
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)在y轴上找出一点P,使的PA+PB的值最小,直接画出点P的位置.
完成下列各题
(1)计算: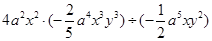 ;
;
(2)计算: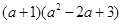 ;
;
(3)因式分解: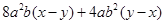 .
.
如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=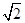 .现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:在△DEF运动过程中,△AEM能否构成等腰三角形?若能,请求出BE的长;若不能,请说明理由.
.现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:在△DEF运动过程中,△AEM能否构成等腰三角形?若能,请求出BE的长;若不能,请说明理由.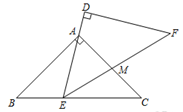
如图,将长方形纸片ABCD沿着EF折叠,使得点C与点A重合.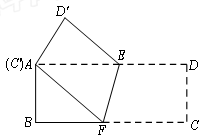
(1)求证:AE=AF;
(2)若AB=3,BC=9,试求CF的长;
(3)在(2)的条件下,试求EF的长.
如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.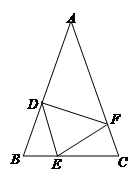
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.