据交管部门统计,高速公路超速行驶是引发交通事故的主要原因.我县某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,渝黔高速公路某路段的限速是:每小时80千米(即最高时速不超过80千米),如图,他们将观测点设在到公路l的距离为0.1千米的P处.这时,一辆轿车由綦江向重庆匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒(注:3秒= 小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)
小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)
(·湖北襄阳,21题)如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?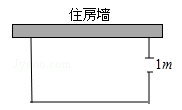
(·湖北荆门,23题,分)甲经销商库存有1200套A品牌服装,每套进价400元,每套售价500元,一年内可卖完,现市场流行B品牌服装,每套进价300元,每套售价600元,但一年内只允许经销商一次性订购B品牌服装,一年内B品牌服装销售无积压,因甲经销商无流动资金可用,只有低价转让A品牌服装,用转让来的资金购进B品牌服装,并销售,经与乙经销商协商,甲、乙双方达成转让协议,转让价格y(元/套)与转让数量x(套)之间的函数关系式为 (
(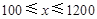 ),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).
),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).
(1)求转让后剩余的A品牌服装的销售款 (元)与x(套)之间的函数关系式;
(元)与x(套)之间的函数关系式;
(2)求B品牌服装的销售款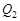 (元)与x(套)之间的函数关系式;
(元)与x(套)之间的函数关系式;
(3)求W(元)与x(套)之间的函数关系式,并求W的最大值.
(·湖北黄冈,23题,分)(10 分)我市某风景区门票价格如图所示黄冈赤壁旅游公司有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120 人,乙团队人数不超过50 人.设甲团队人数为x 人,如果甲、乙两团队分别购买门票,两团队门票款之和为W 元.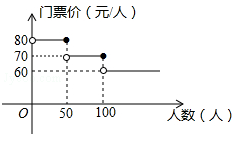
(1)求W 关于x 的函数关系式,并写出自变量x 的取值范围;
(2)若甲团队人数不超过100 人,请说明甲、乙两团队联合购票比分别购票最多可节约多少钱;
(3“) 五一”小黄金周之后,该风景区对门票价格作了如下调整:人数不超过50 人时,门票价格不变;人数超过50 人但不超过100 人时,每张门票降价a 元;人数超过100 人时,每张门票降价2a 元.在(2)的条件下,若甲、乙两个旅行团队“五一”小黄金周之后去游玩,最多可节约3400 元,求a 的值.
(·湖北黄冈,20题,分)如图,在一次军事演习中,蓝方在一条东西走向的公路上的A 处朝正南方向撤退,红方在公路上的B 处沿南偏西60°方向前进实施拦截.红方行驶1000 米到达C 处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D 处成功拦截蓝方.求拦截点D 处到公路的距离(结果不取近似值).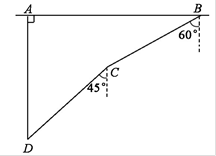
(·湖北黄冈,16题,分)已知A,B两件服装的成本共500元,鑫洋服装店老板分别以30%和20%的利润率定价后进行销售,该服装店共获利130 元,问A,B两件服装的成本各是多少元?