“为了迎接太空时代的到来,美国国会通过一项计划:在2050年前建造成太空升降机,就是把长绳的一端搁置在地球的卫星上,另一端系住升降机,放开绳,升降机能到达地球上,人坐在升降机里。科学家控制卫星上的电动机把升降机拉到卫星上。已知地球表面的重力加速度g=10m/s2,地球半径R=6400km,地球自转周期为24h。某宇航员在地球表面用体重计称得体重为800N,站在升降机中,某时刻当升降机以加速度a=10m/s2垂直地面上升,这时此人再一次用同一体重计称得视重为850N,忽略地球公转的影响,根据以上数据( )
| A.如果把绳的一端搁置在同步卫星上,可知绳的长度至少有多长 |
| B.可以求出升降机此时距地面的高度 |
| C.可以求出升降机此时所受万有引力的大小 |
| D.可以求出宇航员的质量 |
如图所示是一物体的s-t图象,则该物体在6 s内的路程是 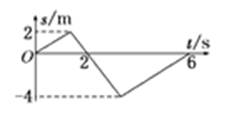
| A.0 m | B.2 m | C.4 m | D.12 m |
下列说法正确的是(填入正确答案标号,选对1个得3分,选对2个得4分,选对3个得6分。每错一个扣3分,最低得0分)
| A.原子的核式结果模型是汤姆逊最早提出的 |
B.铀核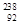 U衰变为铅核 U衰变为铅核 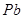 的过程,要经过8次 的过程,要经过8次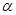 衰变和6次 衰变和6次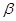 衰变 衰变 |
C.一个氢原子从量子数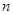 =3的激发态跃迁到基态时最多可辐射3种不同频率的光子 =3的激发态跃迁到基态时最多可辐射3种不同频率的光子 |
| D.一束光照射到某种金属上不能发生光电效应,可能因为光的强度太小 |
E.考古专家发现某一骸骨中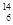 C的含量为活着的生物体中
C的含量为活着的生物体中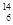 C的1/4,已知
C的1/4,已知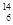 C的半衰期为5730年,则确定该生物死亡时距今越11460年
C的半衰期为5730年,则确定该生物死亡时距今越11460年
一列简谐横波沿 轴正方向传播,在
轴正方向传播,在 秒与
秒与 秒两个时刻,在
秒两个时刻,在 轴上(-3m,3m)区间的波形完全相同,如图所示.并且图中M、N两质点在t秒时位移均为
轴上(-3m,3m)区间的波形完全相同,如图所示.并且图中M、N两质点在t秒时位移均为 ,下列说法中不正确的是( )
,下列说法中不正确的是( )
| A.该波的最大波速为20m/s |
| B.(t+0.1)秒时刻,x=-2m处的质点位移一定是a |
| C.从t秒时刻起,x=2m处的质点比x=2.5m的质点先回到平衡位置 |
| D.从t秒时刻起,在质点M第一次到达平衡位置时,质点N恰好到达波峰 |
E.该列波在传播过程中遇到宽度为d=3m的狭缝时会发生明显的衍射现象
(多选)下列说法正确的是(填正确的答案标号。选对1个得3分,选对2个得4分,选对3个得6分。每错一个扣3分,最低得0分)
| A.水在涂有油脂的玻璃板上能形成水珠,而在干净的玻璃板上却不能,这是因为油脂使水的表面张力增大的缘故。 |
| B.把一枚针放在水面上,它会浮在水面,这是水表面存在表面张力的缘故 |
| C.在围绕地球飞行的宇宙飞船中,自由漂浮的水滴呈球形,这是表面张力作用的结果 |
| D.当两玻璃板间夹有一层水膜,在垂直于玻璃板的方向很难将玻璃板拉开,这是由于水膜具有表面张力的缘故 |
E.在毛细现象中,毛细管中的液面有的升高,有的降低,这与液体的种类和毛细管的材质有关
如图甲所示,倾角为θ的足够长的传送带以恒定的速率v0沿 逆时针方向运行。t =0时,将质量m =1kg的物体(可视为质 点)轻放在传送带上,物体相对地面的v—t图象如图乙所示。 设沿传送带向下为正方向,取重力加速度g =10m/s2。则
| A.传送带的速率v0=10m/s |
| B.送带的倾角θ=300 |
| C.物体与传送带之间的动摩擦因数µ=0.5 |
| D.0〜2.0s摩檫力对物体做功Wf= -24J |