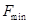水平地面上有一个半径为R的圆形跑道,高为h的平台边缘上P点在地面上P′点的正上方,P′与跑道圆心O的距离为L(L>R),P′AOC各点均在同一水平直线上,如图所示.一辆小车以速率 v在跑道上顺时针运动,已知重力加速度为g,空气阻力不计,小沙袋、小车均可视为质点.则
(1)若从P点水平抛出小沙袋,使其落入小车中,小沙袋被抛出时的初速度应满足什么条件?
(2)若小车经过跑道上A点时(∠AOB=90°),现从P点瞄准B点以某一水平初速度抛出小沙袋,使其落入小车中,则小沙袋被抛出时的初速度V1应满足什么条件?小车的速率 v应满足什么条件?
(l0分).如图所示,一位质量为m ="72" kg的特技演员,在进行试镜排练时,从离地面高 高的楼房窗口跳出后做自由落体,若有一辆平板汽车正沿着下落点正下方所在的水平直线上,以
高的楼房窗口跳出后做自由落体,若有一辆平板汽车正沿着下落点正下方所在的水平直线上,以 的速度匀速前进.已知该演员刚跳出时,平板汽车恰好运动到其前端距离下落点正下方3m处,该汽车车头长2m,汽车平板长4.5 m,平板车板面离地面高
的速度匀速前进.已知该演员刚跳出时,平板汽车恰好运动到其前端距离下落点正下方3m处,该汽车车头长2m,汽车平板长4.5 m,平板车板面离地面高 m,人可看作质点,g取
m,人可看作质点,g取 ,人下落过程中未与汽车车头接触,人与车平板间的动摩擦因数
,人下落过程中未与汽车车头接触,人与车平板间的动摩擦因数
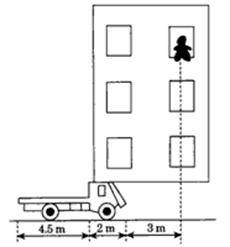
问:(1)人将落在平板车上距车尾端多远处?
(2)假定人落到平板上后立即俯卧在车上不弹起(提示:要考虑该瞬间人水平方向的速度变化,同时因车的质量远大于人的质量,该瞬间车的速度近似不变),司机同时使车开始以大小为 的加速度做匀减速直线运动,直至停止,则人是否会从平板车上滑下?
的加速度做匀减速直线运动,直至停止,则人是否会从平板车上滑下?
(3)人在货车上相对滑动的过程中产生的总热量Q为多少?
(9分)、我国南方大部分省区曾经遭遇了罕见的雪灾,此次灾害过程造成17个省(区、市、兵团)不同程度受灾。尤其是雪灾天气造成输电线被厚厚的冰层包裹(如图甲),使相邻两个铁塔间的拉力大大增加,导致铁塔被拉倒、压塌(如图乙),电力设施被严重损毁,给这些地方群众的生产生活造成了极大不便和巨大损失。当若干相同铁塔等高、等距时,可将之视为如图所示丙的结构模型。已知铁塔(左右对称)质量为 ,塔基宽度为d。相邻铁塔间输电线的长度为L,其单位长度的质量为
,塔基宽度为d。相邻铁塔间输电线的长度为L,其单位长度的质量为 ,输电线顶端的切线与竖直方向成
,输电线顶端的切线与竖直方向成 角。已知冰的密度为
角。已知冰的密度为 ,设冰层均匀包裹输电线上,且冰层的横截面为圆形,其半径为R(输电线的半径可忽略)
,设冰层均匀包裹输电线上,且冰层的横截面为圆形,其半径为R(输电线的半径可忽略)

求(l)因为冰层包裹,每个铁塔塔尖所受的压力将比原来增大多少?
(2)被冰层包裹后,输电线在最高点、最低点的张力
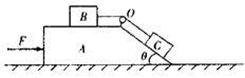
.如图所示,水平面上有一固定着轻质定滑轮O的木块A,它的上表面与水平面平行,它的右侧是一个倾角 的斜面。放置在A上的物体B和物体C通过一轻质细绳相连,细绳的一部分与水平面平行,另一部分与斜面平行。现对A施加一水平向右的恒力F,使A、B、C恰好保持相对静止。已知A、B、C的质量均为m,重力加速度为g,不计一切摩擦,求恒力F的大小。(
的斜面。放置在A上的物体B和物体C通过一轻质细绳相连,细绳的一部分与水平面平行,另一部分与斜面平行。现对A施加一水平向右的恒力F,使A、B、C恰好保持相对静止。已知A、B、C的质量均为m,重力加速度为g,不计一切摩擦,求恒力F的大小。(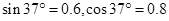 )
)
(8分)、一质量m=2.Okg的小物块以一定的初速度冲上一个足够长的倾角为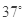 的固定斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机做出了小物块上滑过程的速度一时间图线,如图所示。(取
的固定斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机做出了小物块上滑过程的速度一时间图线,如图所示。(取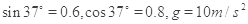 )求 :
)求 : 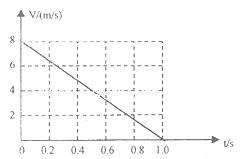
(l)小物块冲上斜面过程中加速度的大小;
(2)小物块与斜面间的动摩擦因数;
(3)小物块向上运动的最大距离。
如图所示,质量不计、劲度系数为k=600N/m的弹簧一端固定在倾角为37°的光滑斜面底端,另一端拴住质量m1="4" kg的物块P,与P紧靠的是质量m2="8" kg的重物Q,系统处于静止。现给Q施加一个方向沿斜面向上的力F,使它从静止开始沿斜面向上做匀加速运动,已知在前0.2 s时间内,F为变力,0.2 s以后,F为恒力。sin37°=0.6,g取10 m/s2;求: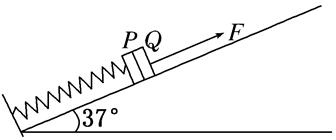
(1)系统静止时,弹簧的形变量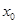
(2)物块Q匀加速运动时的加速度的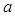 大小
大小
(3)力F的最大值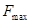 与最小值
与最小值