某大学对该校参加某项活动的志愿者实施“社会教育实施”学分考核，该大学考核只有合格和优秀两个等次.若某志愿者考核为合格，授予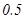
个学分；考核为优秀，授予
个学分.假设该校志愿者甲、乙考核为优秀的概率分别为
、
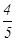，乙考核合格且丙考核优秀的概率为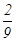
.甲、乙、丙三人考核所得等次相互独立.
（1）求在这次考核中，志愿者甲、乙、丙三人中至少有一名考核为优秀的概率；
（2）记在这次考核中，甲、乙、丙三名志愿者所得学分之和为随机变量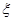
，求随机变量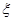的
分布列和数学期望.
设函数
，不等式
的解集为（－1，2）
（1）求
的值；
（2）解不等式
．
已知函数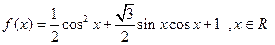
．
（1）求函数
的最小正周期；
（2）求函数在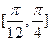
上的最大值和最小值，并求函数取得最大值和最小值时的自变量
的值．
如图，在平面直角坐标系
中，以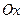
轴为始边做两个锐角
，它们的终边分别与单位圆相交于A、B两点，已知A、B的横坐标分别为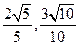
（1）求
的值； （2）求
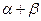的值．
已知椭圆的中心为坐标原点O，焦点在x轴上，过椭圆右焦点F2且斜率为1的直线交椭圆于A、B两点，弦AB的中点为T，OT的斜率为
，
（1）求椭圆的离心率；
（2）设Q是椭圆上任意一点，F1为左焦点，求
的取值范围；
（3）若M、N是椭圆上关于原点对称的两个点，点P是椭圆上任意一点，当直线PN斜率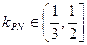
，试求直线PM的斜率
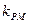的范围。
同时投掷两个骰子，计算下列事件的概率：
（1）事件A：两个骰子点数相同；
（2）事件B：两个骰子点数之和是4的倍数；
（3）事件C：两个骰子点数之差是2 。