小王家是新农村建设中涌现出的 “养殖专业户”．他准备购置80只相同规格的网箱，养殖A、B两种淡水鱼（两种鱼不能混养）．计划用于养鱼的总投资不少于7万元，但不超过7.2万元，其中购置网箱等基础建设需要1.2万元．设他用x只网箱养殖A种淡水鱼，目前平均每只网箱养殖A、B两种淡水鱼所需投入及产业情况如下表：
| 项目类别 |
鱼苗投资 （百元） |
饲料支出 （百元） |
收获成品鱼（千克） |
成品鱼价格 （百元/千克） |
| A种鱼 |
2.3 |
3 |
100 |
0.1 |
| B种鱼 |
4 |
5.5 |
55 |
0.4 |
小王有哪几种养殖方式？
哪种养殖方案获得的利润最大？
根据市场调查分析，当他的鱼上市时，两种鱼的价格会有所变化，A种鱼价格上涨a%（0＜a＜50），B种鱼价格下降20%，考虑市场变化，哪种方案获得的利润最大？（利润=收入-支出．收入指成品鱼收益，支出包括基础建设投入、鱼苗投资及饲料支出）
如图，在平面直角坐标系xOy中，已知点B的坐标为（2，0），点C的坐标为（0，8），sin∠CAB=
, E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连结CE.
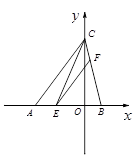
（1）求AC和OA的长；
（2）设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式；
（3）在（2）的条件下试说明S是否存在最大值，若存在，请求出S的最大值，并求出此 时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．
如图，在Rt△ABC中,∠C = 90°，BC=9,CA=12,∠ABC的平分线BD交AC于点D, DE⊥DB交AB于点E. 点O在AB上，⊙O是△BDE的外接圆,交BC于点F,连结EF.求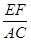
的值.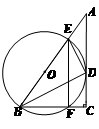
某大型超市为了缓解停车难的问题，建筑设计师提供了楼顶停车场的设计示意图（如图AC与ME平行）．按规定，停车场坡道口上坡要张贴限高标志，以便告知车辆能否安全驶入．请根据下图求出汽车通过坡道口的限高DF的长．（结果精确到0.1m）
（参考数据： sin28°≈0.47，cos28°≈0.88, tan28°≈0.53）
如图，M是
的中点，过点M的弦MN交弦AB于点C，⊙O的半径为4cm，MN＝4
cm．
（1）求圆心O到弦MN的距离；（2）求∠ACM的度数．
如图，四边形ABCD、DEFG都是正方形，连接AE、CG,AE与CG相交于点M，CG与AD相交于点N。求证:
