如图,路灯( 点)距地面8米,身高1.6米的小明从距路灯的底部(
点)距地面8米,身高1.6米的小明从距路灯的底部( 点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
先化简,再求值: ,其中 .
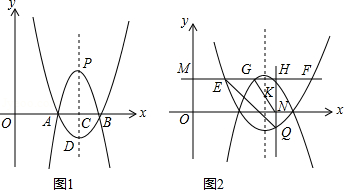
如图1,二次函数 的图象与 轴交于 、 两点(点 在点 的左侧),其对称轴 与 轴交于点 ,它的顶点为点 .
(1)写出点 的坐标 .
(2)点 在对称轴 上,位于点 上方,且 ,以 为顶点的二次函数 的图象过点 .
①试说明二次函数 的图象过点 ;
②点 在二次函数 的图象上,到 轴的距离为 ,当点 的坐标为 时,二次函数 的图象上有且只有三个点到 轴的距离等于 ;
③如图2,已知 ,过点 作 轴的平行线,分别交二次函数 、 的图象于点 、 、 、 (点 、 在对称轴 左侧),过点 作 轴的垂线,垂足为点 ,交二次函数 的图象于点 ,若 ,求实数 的值.
校田园科技社团计划购进 、 两种花卉,两次购买每种花卉的数量以及每次的总费用如下表所示:
|
花卉数量(单位:株) |
总费用(单位:元) |
||
|
|
|
||
|
第一次购买 |
10 |
25 |
225 |
|
第二次购买 |
20 |
15 |
275 |
(1)你从表格中获取了什么信息? (请用自己的语言描述,写出一条即可);
(2) 、 两种花卉每株的价格各是多少元?
公交总站 点)与 、 两个站点的位置如图所示,已知 , , ,求 站点离公交总站的距离即 的长(结果保留根号).

(1)解方程:
(2)解不等式: ,并将它的解集在数轴上表示出来.
