某电视机生产厂家去年销往农村的某品牌电视机每台的售价y（元）与月份x之间满足函数关系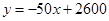
，去年的月销售量p（万台）与月份x之间成一次函数关系，其中两个月的销售情况如下表：
求该品牌电视机在去年哪个月销往农村的销售金额最大？最大是多少？
）由于受国际金融危机的影响，今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了
，且每月的销售量都比去年12月份下降了1.5m%．国家实施“家电下乡”政策，即对农村家庭购买新的家电产品，国家按该产品售价的13%给予财政补贴．受此政策的影响，今年3至5月份，该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下，平均每月的销售量比今年2月份增加了1.5万台．若今年3至5月份国家对这种电视机的销售共给予了财政补贴936万元，求
的值（保留一位小数）．
（参考数据：
，
，
，
）
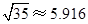用10个球设计一个摸球游戏，使得：
（1）摸到红球的机会是
。
（2）摸到红球的机会是，摸到黄球的机会是
。
（3）你还能设计一个符合下列条件的游戏吗？为什么？
摸到红球的机会是，摸到黄球的机会是，摸到绿球的机会是
。
用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形. 用这两部分纸片除了可以拼成图2中的Rt△BCE外，还可以拼成一些四边形，请你试一试，把拼成的四边形分别画在图3、图4的虚框内。
如图，已知：AB⊥BD，ED⊥BD，AB=CD，BC=DE，那么AC与CE有什么关系？写出你的猜想并说明理由。
观察下面的式子：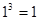
，
，
，
，
，
，
，
，
……
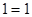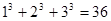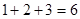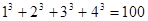（1）猜一猜
等于什么？
（1）猜一猜
等于什么？
（2）写出
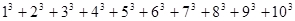的值.
如图，直线AC∥DF，C、E分别在AB、DF上，小华想知道∠ACE和∠DEC是否互补，但是他有没有带量角器，只带了一副三角板，于是他想了这样一个办法：首先连结CF，再找出CF的中点O，然后连结EO并延长EO和直线AB相交于点B，经过测量，他发现EO＝BO，因此他得出结论：∠ACE和∠DEC互补，而且他还发现BC＝EF。
以下是他的想法，请你填上根据。小华是这样想的：
因为CF和BE相交于点O，
根据得出∠COB＝∠EOF；
而O是CF的中点，那么CO＝FO，又已知 EO＝BO，
根据得出△COB≌△FOE，
根据得出BC＝EF，
根据得出∠BCO＝∠F，
既然∠BCO＝∠F，根据出AB∥DF，
既然AB∥DF，根据得出∠ACE和∠DEC互补.