已知抛物线的顶点是C(0，a)（a>0，a为常数），并经过点(2a，2a)，点D(0，2a)为一定点．
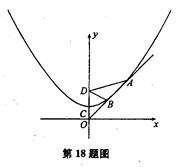
求含有常数a的抛物线的解析式
设点P是抛物线上任意一点，过P作PH⊥x轴，垂足是H，求证：PD＝PH；
设过原点O的直线l与抛物线在第一象限相交于A、B两点．若DA＝2DB，且S△ABD＝4
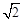，求a的值．
如图所示，点A、C在等腰直角三角形HBE的直角边BH和BE上，且AB=BC，CF⊥HE。EF⊥AE于E。试探究线段AE、EF的数量关系，并证明你的结论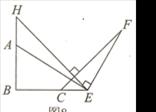
一家蔬菜公司收购某种绿色蔬菜140吨，准备加工后进行销售，销售后获利的情况如右图所示
已知该公司的加工能力是：每天能精加工10吨或粗加工20吨。但两种加工一天之内不能同时进行受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售。（1）若要求12天刚好加工完140吨蔬菜，则该公司应安排几天精加工，几天粗加工
（2）若要求在不超过9天的时间内，将140吨蔬菜全部加工完，则加工这批蔬菜销售后最多能获得多少利润？此时应该如何分配这批蔬菜精、粗加工的时间？
某校八年级进行了一次数学测试，教务处抽取10%的学生成绩进行统计，结果如图7所示，（其中规定86分以上为优秀，76分～85分为良好；60～75为几个；59分以下为不及格）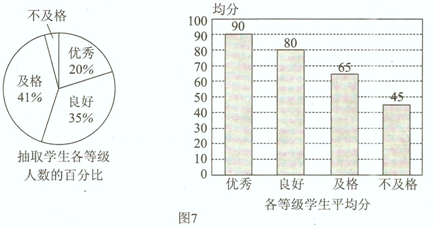
（1）在抽取的学生中，不及格人数为
（2）小明按以下方法计算出所抽取学生数学测试成绩的平均分是：（90+80+65+45）÷4=70.根据所学的统计知识，判断小明的计算是否正确，若不正确，请写出正确的算式并计算出结果
（3）若抽取的学生中不及格学生的成绩恰好等于某一个优秀学生的分数，请估算出该校八年级优秀等级学生的人数
解不等式组
并把解集在数轴上表示出来
（本小题满分9分）
解不等式组
并在所给的数轴上表示出其解集．