(本小题8分)
我省课改实验区于2005年起实行初中毕业生综合素质评价,结果分为A,B,C,D四个等级。我省某区教育局为了解评价情况,从全区3600名初三毕业生中任意抽取了200名学生的评价结果进行统计,得到如图所示扇形统计图:
根据图中提供的信息,(1)请你求出样本中评定为D等级的学生占样本人数的百分之几?有多少人?
(2)请你说明样本中众数落在哪一个等级?估计该区初三毕业生中众数所在等级的总人数大约是多少?
一个不透明的口袋里装着红、黄、绿三种只有颜色不同的球,其中红球有2个,黄球有1个,从中任意摸出1球是红球的概率为 .
.(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出l球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.
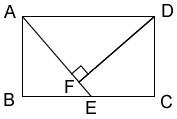
如图,在矩形ABCD中,AB=3cm,AD=4cm,点E是BC上一动点(不与B、C重合),且DF⊥AE,垂足为F. 设AE=xcm,DF=ycm.(1)求证:△DFA∽△ABE;
(2)试求y与x之间的函数关系式,并求出自变量的取值范围.

先化简式子(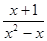 -
-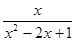 )÷
)÷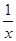 ,然后请选取一个你最喜欢的x值代入求出这个式子的值.
,然后请选取一个你最喜欢的x值代入求出这个式子的值.
如图,已知A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC。且已知AB=CD。(1)试问DB平分EF能成立吗?请说明理由。
(2)若△DEC的边EC沿AC方向移动,其余条件不变,如图,上述结论是否仍成立?请说明理由。