已知一元二次方程x2+ax+a-2=0.
(1)求证:不论a为何实数,此方程总有两个不相等的实数根;
(2)设a<0,当二次函数y=x2+ax+a-2的图象与x轴的两个交点的距离为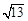 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;
(3)在(2)的条件下,若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为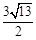 ,若存在求出P点坐标,若不存在请说明理由.
,若存在求出P点坐标,若不存在请说明理由.
计算(每小题4分,共8分):
(1)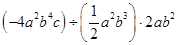
(2)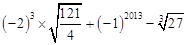
商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价 进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案.
进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案.
如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系﹒
(2)写出超市的坐标(小正方形网格的单位长度为1)﹒
(3)请将体育场、宾馆和火车站看作三点,用线段连接起来,得到△ABC,然后将此三角形向下平移4个单位,再画出平移后的△A′B′C′,并计算△A′B′C′的面积﹒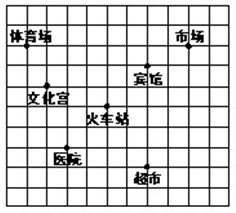
为了了解重庆一中初2014级学生的跳绳成绩,琳琳老师随机调查了该年级开学体育模拟考试中部分同学的跳绳成绩,并绘制成了如图所示的条形统计图和扇形统计图.请你根据图中提供的信息完成下列各题: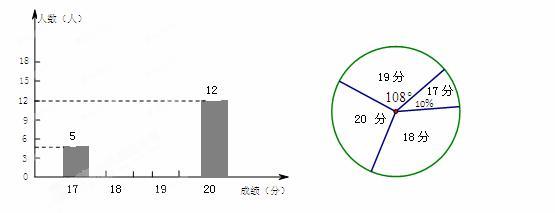
(1)求被调查同学跳绳成绩的中位数,并补全上面的条形统计图;
(2)如果我校初三年级共有学生2025人,估计跳绳成绩能得18分的学生约有多少人?
已知关于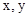 的方程组
的方程组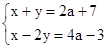
(1)若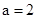 ,求方程组的解;
,求方程组的解;
(2)若方程组的解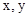 满足
满足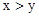 ,,求
,,求 的取值范围并化简
的取值范围并化简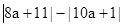 ;
;