已知一次函数的图象与双曲线 交于两点的坐标分别为(
交于两点的坐标分别为( ,
, )、(
)、( ,-1);
,-1);求该一次函数的解析式
描出函数草图,根据图象写出使一次函数的值大于反比例函数的值的
 的取值范围.
的取值范围.
如图,在平面直角坐标系xOy中,已知点B的坐标为(2,0),点C的坐标为(0,8),sin∠CAB= , E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连结CE.
, E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连结CE.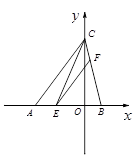
(1)求AC和OA的长;
(2)设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式;
(3)在(2)的条件下试说明S是否存在最大值,若存在,请求出S的最大值,并求出此 时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
如图,在Rt△ABC中,∠C = 90°,BC=9,CA=12,∠ABC的平分线BD交AC于点D, DE⊥DB交AB于点E. 点O在AB上,⊙O是△BDE的外接圆,交BC于点F,连结EF.求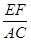 的值.
的值.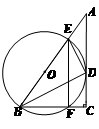
某大型超市为了缓解停车难的问题,建筑设计师提供了楼顶停车场的设计示意图(如图AC与ME平行).按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.请根据下图求出汽车通过坡道口的限高DF的长.(结果精确到0.1m)
(参考数据: sin28°≈0.47,cos28°≈0.88, tan28°≈0.53)
如图,M是 的中点,过点M的弦MN交弦AB于点C,⊙O的半径为4cm,MN=4
的中点,过点M的弦MN交弦AB于点C,⊙O的半径为4cm,MN=4 cm.
cm.
(1)求圆心O到弦MN的距离;(2)求∠ACM的度数.
如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD相交于点N。求证:
