阅读下列文字与例题：
将一个多项式分组后，可提公因式或运用公式继续分解的方法是分组分解法．
例如：（1）am+an+bm+bn=（am+bm）+（an+bn）=m（a+b）+n（a+b）=（a+b）（m+n）
（2）x2﹣y2﹣2y﹣1=x2﹣（y2+2y+1）=x2﹣（y+1）2=（x+y+1）（x﹣y﹣1）
试用上述方法分解因式a2+2ab+ac+bc+b2= ．
如图，已知函数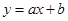
和
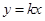的图象交于点P, 则根据图象可得，关于
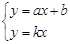的二元一次方程组的解是___________.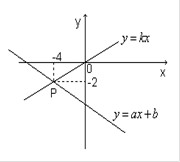
函数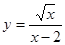
中自变量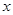
的取值范围是___________.
根据指令[s,A] (s≥0, 0º<A<180º), 机器人在平面上能完成下列动作: 先原地逆时针旋转角度A, 再朝其面对的方向沿直线行走距离s. 现机器人在直角坐标系的坐标原点, 且面对x轴正方向. (1) 若给机器人下了一个指令[4,600]，则机器人应移动到点____； (2
) 请你给机器人下一个指令 ____, 使其移动到点
(-5,5).
直角三角形纸片的两直角边BC、AC的长分别为6、8，现将
如图那样折叠，使点
与点
重合，折痕为
，则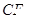
的长为________．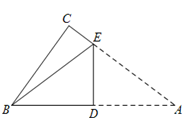
小明用30元钱买笔记本和练习本共30本，已知每本笔记本4元，练习本每本4角，那么他最多能买笔记本_______本。