如图:在平面直角坐标系中,将长方形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB=3,AD=6,将纸片沿过点M的直线折叠(点M在边AB上),使点B落在边AD上的E处(若折痕MN与x轴相交时,其交点即为N),过点E作EQ⊥BC于Q,交折痕于点P。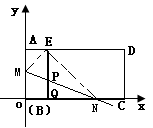
(1)①当点 分别与AB的中点、A点重合时,那么对应的点P分别是点
分别与AB的中点、A点重合时,那么对应的点P分别是点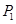 、
、 ,则
,则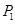 ( , )、
( , )、 ( , );②当∠OMN=60°时,对应的点P是点
( , );②当∠OMN=60°时,对应的点P是点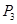 ,求
,求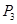 的坐标;
的坐标;
(2)若抛物线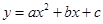 ,是经过(1)中的点
,是经过(1)中的点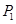 、
、 、
、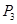 ,试求a、b、c的值;
,试求a、b、c的值;
(3)在一般情况下,设P点坐标是(x,y),那么y与x之间函数关系式还会与(2)中函数关系相同吗(不考虑x的取值范围)?请你利用有关几何性质(即不再用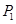 、
、 、
、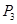 三点)求出y与x之间的关系来给予说明.
三点)求出y与x之间的关系来给予说明.
如图,在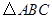 中,
中,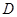 是
是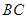 边的中点,
边的中点,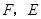 分别是
分别是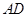 及其延长线上的点,
及其延长线上的点,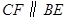 .
.求证:
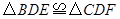 .
.请连结
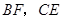 ,试判断四边形
,试判断四边形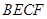 是何种特殊四边形,并说明理由.
是何种特殊四边形,并说明理由.
张老汉为了与客户签订购销合同,需对自己的鱼塘中的鱼的总量进行估计,他采用了这样的方法:第一次捞出 100 条鱼,称得重量为 184kg,并把每条鱼作上记号放入水中;当它们完全混合于鱼群后,又捞出 200 条,称得重量为 416 kg,且带有记号的鱼有 20 条。张老汉采用这样的方法是否可靠?为什么?
张老汉的鱼塘中大约共有鱼多少条?共重多少 kg?
小明在如图所示粗糙的平面轨道上滚动一个半径为8cm的圆盘,已知,AB与CD是水平的,BC与水平方向夹角为600,四边形BCDE是等腰梯形,CD=EF=AB=BC=40cm,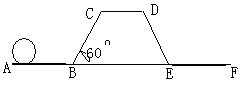
请作出小明将圆盘从A点滚动至F点其圆心所经过的路线示意图
求出(1)中所作路线的长度。
如图,面积为8的矩形ABOC的边OB、OC分别在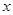 轴、
轴、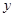 轴的正半轴上,点A在双曲线
轴的正半轴上,点A在双曲线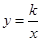 的图象上,且AC=2
的图象上,且AC=2
求
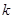 值
值将矩形ABOC以B旋转中心,顺时针旋转90°后得到矩形FBDE,双曲线交DE于M点,交EF于N点,求△MEN的面积
如图,四边形ABCD中,∠A=90°,AD∥BC,BE⊥CD
于E交AD的延长线于F,DC=2AD,AB=BE.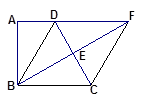
求证:AD=DE
判断四边形BCFD的形状并说明理由.