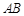设函数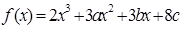 在
在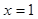 及
及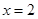 时取得极值.
时取得极值.
(1)求a、b的值;
(2)当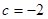 时,求函数
时,求函数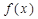 在区间
在区间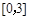 上的最大值.
上的最大值.
已知函数
(I)求函数 的最小正周期;
的最小正周期;
(II)求函数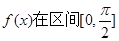 上的最大值与最小值.
上的最大值与最小值.
已知等差数列 的每一项都有
的每一项都有 求数列
求数列 的前n项和
的前n项和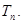
在数列 和
和 中,
中, ,
,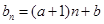 ,
,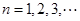 ,其中
,其中 且
且 ,
,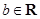 .设
.设 ,
,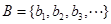 ,试问在区间
,试问在区间 上是否存在实数
上是否存在实数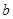 使得
使得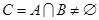 .若存在,求出
.若存在,求出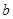 的一切可能的取值及相应的集合
的一切可能的取值及相应的集合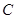 ;若不存在,试说明理由.
;若不存在,试说明理由.
学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且 .
.
(1)求文娱队的队员人数;
(2)写出 的概率分布列并计算
的概率分布列并计算
在直角坐标系 中,直线
中,直线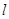 的参数方程为
的参数方程为 (
(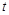 为参数),若以直角坐标系
为参数),若以直角坐标系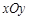 的
的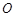 点为极点,
点为极点,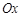 为极轴,且长度单位相同,建立极坐标系,得曲线
为极轴,且长度单位相同,建立极坐标系,得曲线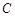 的极坐标方程为
的极坐标方程为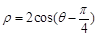 .
.
(1)求直线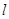 的倾斜角;
的倾斜角;
(2)若直线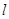 与曲线
与曲线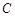 交于
交于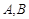 两点,求
两点,求