已知椭圆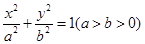 的左、右焦点分别是
的左、右焦点分别是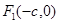 、
、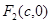 ,离心率为
,离心率为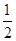 ,椭圆上的动点
,椭圆上的动点 到直线
到直线 的最小距离为2,延长
的最小距离为2,延长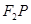 至
至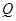 使得
使得 ,线段
,线段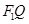 上存在异于
上存在异于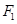 的点
的点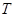 满足
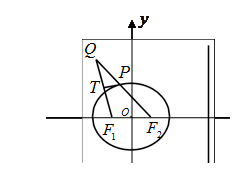
满足 .
.
(1) 求椭圆的方程;
(2) 求点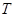 的轨迹
的轨迹 的方程;
的方程;
(3) 求证:过直线 上任意一点必可以作两条直线
上任意一点必可以作两条直线
与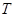 的轨迹
的轨迹 相切,并且过两切点的直线经过定点.
相切,并且过两切点的直线经过定点.
设不等式组 所表示的平面区域为
所表示的平面区域为 ,记
,记 内的格点(格点即横坐标和纵坐标均为整数的点)的个数为
内的格点(格点即横坐标和纵坐标均为整数的点)的个数为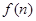 (
( ).
).
(Ⅰ)求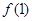 、
、 的值及
的值及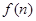 的表达式;
的表达式;
(Ⅱ)设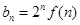 ,
, 为
为 的前
的前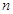 项和,求
项和,求 .
.
已知函数f(x)=ax2+a2x+2b-a3,当x∈(-2,6)时,其值为正,而当x∈(-∞,-2)∪(6,+∞)时,其值为负.
(Ⅰ)求实数a,b的值及函数f(x)的表达式;
(Ⅱ)设F(x)=- f(x)+4(k+1)x+2(6k-1),问k取何值时,函数F(x)的值恒为负值?
f(x)+4(k+1)x+2(6k-1),问k取何值时,函数F(x)的值恒为负值?
.若非零函数 对任意实数
对任意实数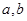 均有¦(a+b)=¦(a)·¦(b),且当
均有¦(a+b)=¦(a)·¦(b),且当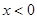 时,
时, .
.
(1)求证: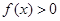 ;
;
(2)求证: 为减函数;
为减函数;
(3)当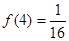 时,解不等式
时,解不等式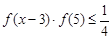
.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.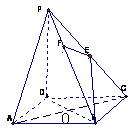
(1)证明 PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
.某飞机制造公司一年中最多可生产某种型号的飞机100架。已知制造x架该种飞机的产值函数为R(x)=3000x-20x2 (单位:万元),成本函数C(x)="500x+4000" (单位:万元)。利润是收入与成本之差,又在经济学中,函数¦(x)的边际利润函数M¦x)定义为:M¦x)=¦(x+1)-¦(x).
①、求利润函数P(x)及边际利润函数MP(x);(利润=产值-成本)
②、问该公司的利润函数P(x)与边际利润函数MP(x)是否具有相等的最大值?