数学课上，李老师出示了如下框中的题目.小敏与同桌小聪讨论后，进行了如下解答：
特殊情况，探索结论. 当点
为
的中点时，确定线段
与
的大小关系，请你直接写出结论： （填“>”,“<”或“=”）.
特例启发，解答题目
解：题目中，与的大小关系是： （填“>”,“<”或“=”）.理由如下：
如图1，过点作
，交
于点
.（请你完成以下解答过程）拓展结论，设计新题
在等边三角形
中，点在直线上，点
在直线
上，且
.若
的边长为1，
，则
的长为 （请你画出图形并直接写出结果，图没画或画错均不得分）.
如图，在△ABC中，∠BAC=90°，AB=AC，AB是⊙O的直径，⊙O交BC于点D，DE⊥AC于点E，BE交⊙O于点F，连接AF，AF的延长线交DE于点P．
（1）求证：DE是⊙O的切线；
（2）求tan∠ABE的值；
（3）若OA=2，求线段AP的长．
在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时x（h）之间的函数图象，根据图象解答以下问题：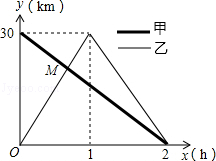
（1）写出A、B两地直接的距离；
（2）求出点M的坐标，并解释该点坐标所表示的实际意义；
（3）若两人之间保持的距离不超过3km时，能够用无线对讲机保持联系，请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围．
如图，在菱形ABCD中，AC为对角线，点E、F分别是边BC、AD的中点．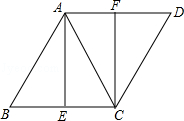
（1）求证：△ABE≌△CDF；
（2）若∠B=60°，AB=4，求线段AE的长．
2013年6月，某中学结合广西中小学阅读素养评估活动，以“我最喜爱的书籍”为主题，对学生最喜爱的一种书籍类型进行随机抽样调查，收集整理数据后，绘制出以下两幅未完成的统计图，请根据图1和图2提供的信息，解答下列问题：
（1）在这次抽样调查中，一共调查了多少名学生？
（2）请把折线统计图（图1）补充完整；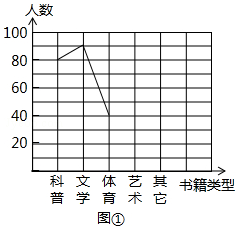
（3）求出扇形统计图（图2）中，体育部分所对应的圆心角的度数；
（4）如果这所中学共有学生1800名，那么请你估计最喜爱科普类书籍的学生人数．
如图，△ABC三个定点坐标分别为A（﹣1，3），B（﹣1，1），C（﹣3，2）．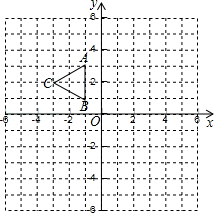
（1）请画出△ABC关于y轴对称的△A1B1C1；
（2）以原点O为位似中心，将△A1B1C1放大为原来的2倍，得到△A2B2C2，请在第三象限内画出△A2B2C2，并求出S△A1B1C1：S△A2B2C2的值．