已知函数y=f(x)在R上为奇函数,且当x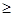 0时,f(x)=
0时,f(x)=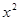 -2x,则f(x)在
-2x,则f(x)在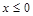 时的解析式是( )
时的解析式是( )
A. f(x)=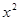 -2x -2x |
B.f(x)=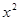 +2x +2x |
C.f(x)= -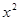 +2x +2x |
D.f(x)= -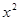 -2x -2x |
已知 是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①
是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:① ②
② ③
③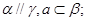 如果命题
如果命题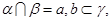 且_______,则
且_______,则 为真命题,则可以在横线处填入的条件是()
为真命题,则可以在横线处填入的条件是()
| A.①或② | B.②或③ | C.①或③ | D.只有② |
由命题“存在x∈R,使e|x-1|-m≤0”是假命题,得m的取值范围是(-∞,a),则实数a的取值是( )
| A.(-∞,1) | B.(-∞,2) | C.1 | D.2 |
已知平面向量a、b,|a|=1,|b|= ,且|2a+b|=
,且|2a+b|= ,则向量a与向量a+b的夹角为( )
,则向量a与向量a+b的夹角为( )
A. |
B. |
C. |
D.π |
存在两条直线 与双曲线
与双曲线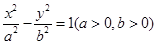 相交于ABCD四点,若四边形ABCD是正方形,则双曲线的离心率的取值范围为( )
相交于ABCD四点,若四边形ABCD是正方形,则双曲线的离心率的取值范围为( )
A. |
B.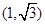 |
C.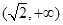 |
D. |
执行如图所示的程序框图,若输出的结果是8,则判断框内m的取值范围是()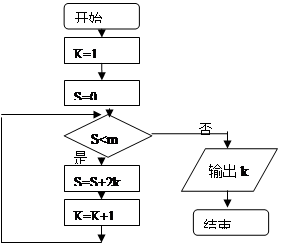
A.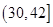 |
B. |
C.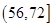 |
D.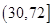 |