解不等式(组)或方程
(1)解不等式 ;
;
(2)解方程 +
+ =1.
=1.
(3)解不等组
反比例函数 为常数,且 的图象经过点 、 .
(1)求反比例函数的解析式及 点的坐标;
(2)在 轴上找一点 ,使 的值最小,求满足条件的点 的坐标.
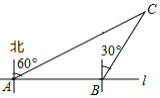
如图,某市郊外景区内一条笔直的公路 经过 、 两个景点,景区管委会又开发了风景优美的景点 .经测量, 位于 的北偏东 的方向上, 位于 的北偏东 的方向上,且 .
(1)求景点 与 的距离;
(2)为了方便游客到景点 游玩,景区管委会准备由景点 向公路 修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)
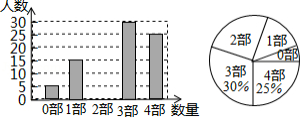
中华文化源远流长,在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中抽取 名学生进行调查.根据调查结果绘制成如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
(1)求 的值;
(2)请将条形统计图补充完整;
(3)若该校共有2000名学生,请估计该校四大古典名著均已读完的人数.
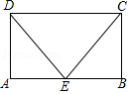
如图,在矩形 中, 是 的中点,连接 、 .
(1)求证: ;
(2)若 , ,求 的周长.
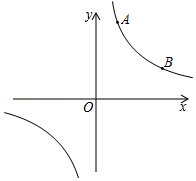
如图,点 为抛物线 上一动点.
(1)若抛物线 是由抛物线 通过图象平移得到的,请写出平移的过程;
(2)若直线 经过 轴上一点 ,且平行于 轴,点 的坐标为 ,过点 作 于 .
①问题探究:如图一,在对称轴上是否存在一定点 ,使得 恒成立?若存在,求出点 的坐标:若不存在,请说明理由.
②问题解决:如图二,若点 的坐标为 ,求 的最小值.
