某展览大厅有3个入口和2个出口,其示意图如下. 参观者从任意一个入口进入,参观结束后从任意一个出口离开.
(1)用树状图表示,小明从进入到离开,对于入口和出口的选择有多少种不同的结果?
(2)小明从入口1进入并从出口A离开的概率是多少?
如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.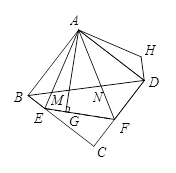
(1)求证:四边形ABCD是正方形;
(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.(3)若EG=4,GF=6,BM=3,求AG、MN的长.
如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.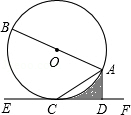
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD•AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
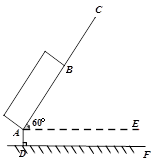
一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,
点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距
离(精确到1cm).(参考数据: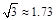 )
)
如图,吴老师不小心把墨水滴在了3个班学生捐款金额的统计表上,只记得:三个班的捐款总金额是7700元,2班的捐款金额比3班的捐款金额多300元.
(1)求2班、3班的捐款金额;
(2)若1班学生平均每人捐款的金额大于48元,小于51元.求1班的学生人数.
A、B两城间的公路长为450千米,甲、乙两车同时从A城出发沿这一公路驶向B城,甲车到达B城1小时后沿原路返回.如图是它们离A城的路程y(千米)与行驶时间 x(小时)之间的函数图像.
(1)求甲车返回过程中y与x之间的函数解析式,并写出x的取值范围;
(2)乙车行驶6小时与返回的甲车相遇,求乙车的行驶速度.