观察发现
如题27(a)图,若点A,B在直线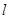 同侧,在直线
同侧,在直线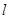 上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线
上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线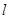 的对称点
的对称点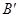 ,连接
,连接 ,与直线
,与直线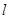 的交点就是所求的点P
的交点就是所求的点P
再如题27(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.
如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这
点就是所求的点P,故BP+PE的最小值为 .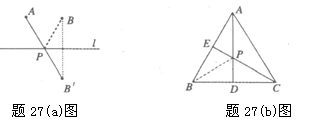
实践运用
如题27(c)图,已知⊙O的直径CD为4,弧AD所对圆心角的度数为60°,点B是弧AD的中点,请你在直径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值.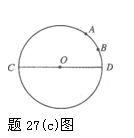
拓展延伸
如题27(d)图,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.保留
作图痕迹,不必写出作法.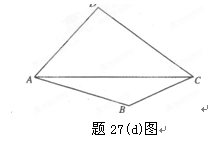
化简求值[(3m-n)2+(3m+n)(3m-n)+6mn]÷2m,其中m=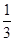 .
.
分解因式
(1)
(2)
(3)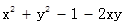
计算:
(1)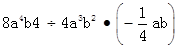
(2)
如图,动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴的正反向运动,3秒后,两点相距15个单位长度。已知动点A,B的速度之比为 (速度单位:单位长度/秒)
(速度单位:单位长度/秒)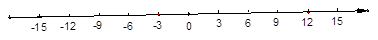
(1)求出两个动点运动的速度,并在数轴上标出A,B两点从原点出发运动3秒时的位置
(2)若A,B两点从(1)中的位置同时按原速度向数轴负方向运动,几秒时,原点恰好在两动点中间?
(3)在(2)中,原点在A,B两点的中间位置时,若A,B两点同时开始向数轴负方向运动时,另一动点C由(2)中点B的位置出发向A运动,当它遇到A后立即返回向点B运动,遇到点B后又立即返回向点A运动....如此往返,直到点B追上点A时,点C立即停止运动。若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始到停止运动,行驶的路程是多少个单位?
为鼓励据居民节约用电,某市电力公司规定了电费的分段计算的方法:每月用电不超过100度,按每度点0.50元计算;每月用电超过100度,超出部分按每度点0.65元计算.设每月用电x度.
(1)若0≤x≤100时,电费为元;若x>100时,电费为__________________元.(用含有x的式子表示);
(2)该用户为了解日用电量,记录了9月第一周的电表读数
| 日期 |
9月1日 |
9月2日 |
9月3日 |
9月4日 |
9月5日 |
9月6日 |
9月7日 |
| 电表读数(度) |
123 |
130 |
137 |
145 |
153 |
159 |
165 |
请你估计该用户9月的电费约为多少元?
(3)该用户采取了节电措施后,10月平均每度电费0.55元,那么该用户10月份用电多少度?