假设地球为密度均匀的球体，若保持密度不变，而将半径缩小1／2，那么地面上的物体所受的重力将变为原来的( )
| A．2倍 | B．1／2 | C．4倍 | D．1／8 |
如图所示，在匀强磁场中有一倾斜的平行金属导轨，导轨间距为l，两导轨间连有一电阻R，导轨平面与水平面的夹角为θ，在两虚线间的导轨上涂有薄绝缘涂层．匀强磁场的磁感应强度大小为B，方向与导轨平面垂直．质量为m的导体棒从h高度处由静止释放，在刚要滑到涂层处时恰好匀速运动．导体棒始终与导轨垂直且仅与涂层间有摩擦，动摩擦因数μ=tanθ，其他部分的电阻不计，重力加速度为g，下列说法正确的是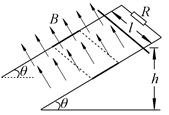
| A．导体棒到达涂层前做加速度减小的加速运动 |
| B．在涂层区导体棒做减速运动 |
C．导体棒到达底端的速度为 |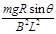
D．整个运动过程中产生的焦耳热为 |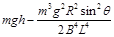
某同学对某种抽水泵中的电磁泵模型进行了研究。如图电磁泵是一个长方体，ab边长为L1，左右两侧面是边长为L2的正方形，在泵头通入导电剂后液体的电阻率为ρ，泵体所在处有方向垂直向外的磁场B，把泵体的上下两表面接在电压为U（内阻不计）的电源上，理想电流表示数为I，若电磁泵和水面高度差为h，不计水在流动中和管壁之间的阻力，重力加速度为g。则
| A．泵体上表面应接电源正极 |
| B．电源提供的电功率为U2L1/ρ |
| C．电磁泵不加导电剂也能抽取不导电的纯水 |
D．在t时间内抽取水的质量为m，这部分水离开泵时的动能为 |
【原创】在研究微型电动机的性能时，可采用右图所示的实验电路。当调节滑动变阻器R，使电动机停止转动时，电流表和电压表的示数分别为2.0A和3.0V；重新调节R，使电动机恢复正常运转时，电流表和电压表的示数分别为3.0A和30.0V。则当这台电动机正常运转时
| A．电动机的内阻为10Ω |
| B．电动机的内阻为2.0Ω |
C．电动机的效率 |
| D．电动机的发热功率为90W |
空间某区域竖直平面内存在电场，电场线分布如图所示。一个质量为m、电量为q，电性未知的小球在该电场中运动，小球经过A点时的速度大小为
，方向水平向右，运动至B点时的速度大小为
。若A、B两点之间的高度差为h，则以下判断中正确的是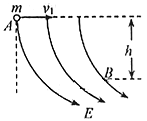
A．A、B两点的电场强度和电势大小关系为
、
B．若
，则电场力一定做正功
C．A、B两点间的电势差为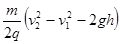
D．小球从A运动到B点的过程中电场力做的功为
理论研究表明第二宇宙速度是第一宇宙速度的
倍。火星探测器悬停在距火星表面高度为h处时关闭发动机，做自由落体运动，经时间t落到火星表面。已知引力常量为G，火星的半径为R。若不考虑火星自转的影响，要使探测器脱离火星飞回地球，则探测器从火星表面的起飞速度至少为
A． |
B． |
C．11.2km/s | D．7.9km/s |