如图，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=900。
求证：PC⊥BC；
求点A到平面PBC的距离。
（本小题满分12分）已知
为圆
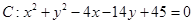上任一点，且点
．
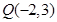（1）若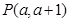
在圆
上，求线段
的长及直线的斜率；
（2）求
的最大值和最小值；
（3）若
,求
的最大值和最小值．
（本小题满分12分）设平面α∥β，两条异面直线AC和BD分别在平面α、β内，线段AB、CD中点分别为M、N，设MN=a，线段AC=BD=2a，求异面直线AC和BD所成的角.
（本小题满分10分）已知函数
=
(2≤
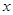≤4)
（1）令
,求y关于t的函数关系式,t的范围.
（2）求该函数的值域.
（本小题满分12分）
已知抛物线C的顶点在原点，焦点在x轴上，且抛物线上有一点
（4
，
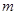）到焦点的距离为5．
（Ⅰ）求抛物线C的方程；
（Ⅱ）若抛物线C与直线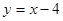
相交于不同的两点A、B，求证：
．
（本小题满分12分）如图，在长方
中，
，
，当E为AB中点时，求二面角
的余弦值．