1930年泡利提出，在β衰变中除了电子外还会放出不带电且几乎没有静质量反中微子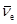
．氚是最简单的放射性原子核，衰变方程为
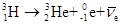，半衰期为12.5年．
（1）下列说法中正确的是 ．
| A．两个氚原子组成一个氚气分子，经过12.5年后，其中的一个氚核一定会发生衰变 |
| B．夜光手表中指针处的氚气灯放出β射线撞击荧光物质发光，可以长时间正常工作 |
| C．氚气在1大气压下，温度低于25.04K时可液化，液化后氚的衰变速度变慢 |
| D．氚与氧反应生成的超重水没有放射性 |
（2）在某次实验中测得一静止的氚核发生β衰变后，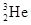
的动量大小为p1，沿反方向运动的电子的动量大小为p2（p1< p2），则反中微子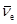的动量大小为 ．若
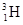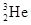、和
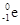的质量分别为m1、m2和m3，光在真空中的传播速度为c，则氚核β衰变释放的能量为 ．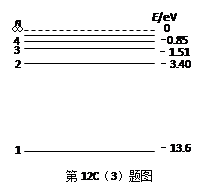
（3）电子撞击一群处于基态的氢原子，氢原子激发后能放出6种不同频率的光子，氢原子的能级如图所示，则电子的动能至少为多大？
如图所示截面为矩形的平行玻璃砖,图中的MN垂直NP,一束单色光从MN上的一点进入玻璃砖后,又从NP上一点B返回空气中,已知入射角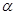
和出射角β｡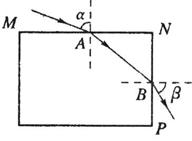
(1)求玻璃砖的折射率｡
(2)若已知n=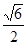
,0≤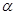≤π/2,求β的最小值｡
如图所示是t＝0时刻的波形图，此时波传到x＝3.0 m处，质点P正向y轴正方向运动，经0.3 s第一次达到波谷位置．求：
(1)波的传播方向及波速；
(2)x＝5.0 m处质点Q在0～0.7 s内通过的路程及0.7 s时的位移．
小明站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为m的小球，甩动手腕，使球在竖直平面内做圆周运动。当球某次运动到最低点时，绳恰好断掉，球飞行水平距离d后落地。如图所示。已知握绳的手离地面高度为d，手与球之间的绳长为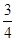
d,重力加速度为g。忽略手的运动半径和空气阻力，绳能承受的最大拉力为定值。
（1）求绳断开时小球的速度；
（2）求绳能承受的最大拉力；
（3）改变绳长，使球重复上述运动，若绳仍在球运动到最低点时恰好断掉，求小球飞行的水平距离最大，绳长应为多少？最大水平距离为多少？
如图为修建高层建筑常用的塔式起重机.在起重机将质量m＝5×103 kg的重物竖直吊起的过程中，重物由静止开始向上做匀加速直线运动，加速度a＝0.2 m/s2，当起重机输出功率达到其允许的最大值时，保持该功率直到重物做vm＝1.02 m/s的匀速运动.取g＝10 m/s2，不计额外功.求：
(1)起重机允许输出的最大功率；
(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率.
两个星球组成双星，它们在相互之间的万有引力作用下，绕连线上某点做周期相同的匀速圆周运动，现测得两个星球中心距离为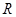
，其运动周期为
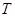，万有引力常量为
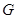，求两个星球的总质量。