某运输部门规定:办理托运,当一件物品的重量不超过a千克(a<18)时,需付基础费30元和保险费b元;为了限制过重物品的托运,当一件物品超过a千克时,除了付以上基础费和保险费外,超过部分还需每千克付c元的超重费.设某件物品的重量为x千克
当0<x≤a时,支付费用为___________(用含b的代数式表示);
当x>a时,支付费用为 ____________(用含x和a、b、c的代数式表示);
甲、乙、丙三人各托运一件物品,物品的重量与支付费用如下表所示:

①根据以上提供的信息确定a、b、c的值;
②试问在物品可拆分的情况下,用不超过120元的费用能否托运50千克的物品?若能,请你设计出一种最省的托运方案;若不能,请你说明理由.
为了解某地九年级男生的身高情况,从该地的一所中学选取容量为60的样本(60名学生的身高.单位:厘米),分组情况如下:
求出表中a和m的值.
如图,要在长100m,宽90m的长方形绿地上修建宽度相同的道路,6块绿地面积共8 448m2,求道路的宽.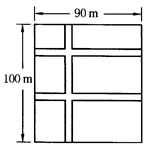
如图,AB⊥BC,AB=10cm,点M以1cm/s的速度从点A开始沿AB边向点B运动,点N同时以2cm/s的速度从点B开始沿BC边向点C运动,则当点M运动多少时间时,△BMN的面积等于24cm2?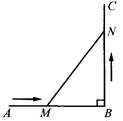
将一块长比宽多3cm的长方形铁皮四角各剪去一个边长为4cm的小正方形,做成一个无盖的盒子.已知盒子的体积是280cm3,求原铁皮的边长.
一个两位数,个位数字与十位数字之和是5,十位上的数字与个位上的数字对调后所得的数与原数相乘,得736,求这个两位数.