如图,已知,△ABC与△DCE为一小一大的两个等腰直角三角形,顶点C互相重合。连结AE、BD交于O,其中△ABC保持不动,当△DCE绕点C旋转时,∠AOB的大小有无变化?证明你的结论.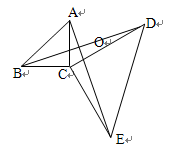
如图,△ABC中,AB=AC,作以AB为直径的⊙O与边BC交于点D,过点D作⊙O的切线,分别交AC、AB的延长线于点E、F.
(1)求证:EF⊥AC;
(2)若BF=2,CE=1.2,求⊙O的半径.
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据PM2.5检测网的空气质量新标准,从德州市2013年全年每天的PM2.5日均值标准值(单位:微克/立方米)监测数据中随机地抽取25天的数据作为样本,并根
据检测数据制作了尚不完整的频数分布表和条形图:

(1)求出表中m,n,a的值,并将条形图补充完整;
(2)以这25天的PM2.5日均值来估计该年的空气质量情况,估计该年(365天)大约有多少天的空气质量达到优或良;
(3)请你结合图表评价一下我市的空气质量情况.
如图,已知矩形OABC的A点在x轴上,C点在y轴上,OC=6,OA=10.
(1)在BC边上求作一点E,使OE=OA;(保留作图痕迹,不写画法)
(2)求出点E的坐标.
化简求值: ,其中x=
,其中x= .
.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点A坐标为(-1,0).则下面的四个结论:
①2a+b=0;②4a+2b+c>0;③B点坐标为(4,0);④当x<-1时,y>0.
其中正确的是( )
A.①② B.③④ C.①④ D.②③