列方程解应用题
某水果批发商欲将A市的一批水果运往B市销售，有火车和汽车两种运输工具，运输过程中的损耗均为160元/时。其它主要参考数据如下：
| 运输工具 |
平均速度 （千米/时） |
运费 （元/千米） |
装卸费用 （元） |
| 火车 |
100 |
18 |
1800 |
| 汽车 |
80 |
22 |
1000 |
（1）如果汽车的总支出费用比火车费用多960元，你知道A市与B市之间的路程是多少千米吗？请你列方程解答。
（2）如果A市与C市之间的距离为300千米，要想将这批水果运往C市销售。选择哪种运输工具比较合算呢？说明你的理由。
已知：梯形ABCD中，AD∥BC,∠ABC=90°，BE⊥CD于点E．DP⊥CB于点P,连接AP、PE.如图1，若∠C=45°，求证：AP=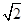 
AE．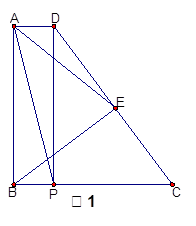
如图2，若∠C=60°，直接写出线段AP、AE的数量关系．
在（1）的条件下，将线段EA绕点E顺时针旋转得到线段EA′，使∠DEA′=∠DAE,直线EA′分别与线段BA延长线、线段BC交于点N、点K,已知AD=1,EK=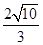
.求线段NE的长．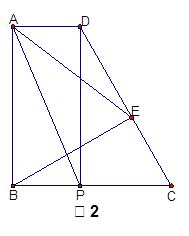
如图，平面直角坐标系中，点A（4，0），直线AB与y轴交于点B，S△AOB=6，点P从点A出发，以每秒1个单位的速度沿x轴正方向运动．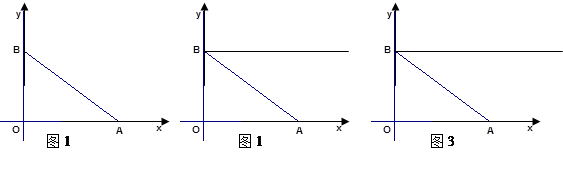
求B点坐标。
过点B作射线L∥x轴，动点Q从B出发，以每秒2个单位的速度，沿射线L运动．若动点P、Q同时运动，过点A作AC⊥AB,射线AC与射线PQ、射线L分别交于点C、K．设运动时间为t秒，线段KQ的长为y个单位．求y与t的函数关系式，并直接写出自变量t的取值范围．
在（2）的条件下，若D为BC中点．在点P、Q运动过程中是否存在t值， 以A、C、D、Q为顶点的四边形是平行四边形，若存在，求出t值；若不存在，请说明理由．
小明利用课余时间回收废品，将卖得的钱去购买5本大小不同的两种笔记本，要求共花钱不超过28元，且购买的笔记本的总页数不低于340页，两种笔记本的价格和页数如下表．
| 大笔记本 |
小笔记本 |
|
| 价格（元/本） |
a |
b |
| 页数（页/本） |
100 |
60 |
(1)文具店一本大笔记本与一本小笔记本的售价和为11元，用12元钱购买的大笔记本数量与用10元钱购买的小笔记本数量相同．求a、b的值．
(2)在（1）的条件下，为了节约资金，小明应购买两种笔记本各多少本？
我校非毕业学年举行“体育节”，同学们积极参加体育锻炼，小铭就本班同学“我最喜爱的体育项目”进行了一次调查统计，下面是他通过收集数据后，绘制的两幅不完整的统计图．请你根据图中提供的信息，解答以下问题：
（1）求该班共有多少名学生；
（2）补全条形统计图；
（3）若我校非毕业学年有5800名学生，请计算出最喜爱“乒乓球”部分的学生人数．
如图，某小区广场要设计一个矩形花坛，花坛的长、宽分别为30 m、20 m，花坛中有一横一纵的两条通道，余下部分种植花卉．横纵通道的宽度均为x m．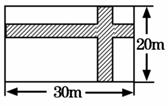
（1）求两条通道的总面积S与x的函数关系式，不要求写出自变量x的取值范围；
（2）当种植花卉面为551米2时，求横、纵通道的宽度为多少米？