如图,在平面直角坐标系 中,抛物线
中,抛物线 与
与 轴交于点
轴交于点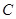 ,与
,与 轴交于
轴交于 两点,直线
两点,直线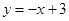 恰好经过
恰好经过 两点.
两点.求出抛物线
 的解析式,并写出抛物线的对称轴;
的解析式,并写出抛物线的对称轴;点
 在抛物线的对称轴上,抛物线顶点为D若
在抛物线的对称轴上,抛物线顶点为D若 ,求点
,求点 的坐标.
的坐标.
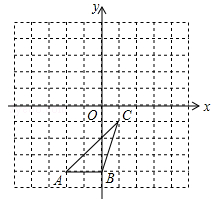
(南宁)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2,请在图中画出△A2BC2,并求出线段BC旋转过程中所扫过的面积(结果保留π).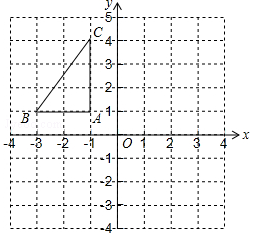
(贵港)已知:△ABC是等腰三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=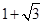 ,PA=
,PA=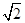 ,则:①线段PB= ,PC= ;
,则:①线段PB= ,PC= ;
②猜想: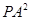 ,
,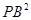 ,
,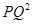 三者之间的数量关系为 ;
三者之间的数量关系为 ;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足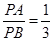 ,求
,求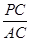 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)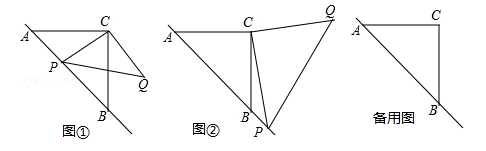
(南宁)在平面直角坐标系中,已知A、B是抛物线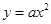 (
(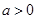 )上两个不同的点,其中A在第二象限,B在第一象限,
)上两个不同的点,其中A在第二象限,B在第一象限,
(1)如图1所示,当直线AB与x轴平行,∠AOB=90°,且AB=2时,求此抛物线的解析式和A、B两点的横坐标的乘积.
(2)如图2所示,在(1)所求得的抛物线上,当直线AB与x轴不平行,∠AOB仍为90°时,A.B两点的横坐标的乘积是否为常数?如果是,请给予证明;如果不是,请说明理由.
(3)在(2)的条件下,若直线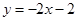 分别交直线AB,y轴于点P、C,直线AB交y轴于点D,且∠BPC=∠OCP,求点P的坐标.
分别交直线AB,y轴于点P、C,直线AB交y轴于点D,且∠BPC=∠OCP,求点P的坐标.
(贺州)如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.若DE=4,BD=8.
(1)求证:AF=EF;
(2)求证:BF平分∠ABD.
(桂林)如图,△ABC各顶点的坐标分别是A(﹣2,﹣4),B(0,﹣4),C(1,﹣1).
(1)在图中画出△ABC向左平移3个单位后的△A1B1C1;
(2)在图中画出△ABC绕原点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,AC边扫过的面积是 .