已知两直线l1：mx＋8y＋n＝0和l2：2x＋my－1＝0.试确定m、n的值，分别使
(1)l1与l2相交于点P(m，－1)；
(2)l1∥l2；
(3)l1⊥l2且l1在y轴上的截距为－1.
（1）若离心率为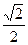
，求椭圆的方程；
（2）当
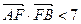时，求椭圆离心率的取值范围
（1）求样本中产品净重小于100克的频率；
（2）已知样本中产品净重小于100克的件数是72，求样本中净重（单位：克）在[100，104)范围内的件数；
（3）若这批产品共有10000件，试估计其中净重（单位：克）在[104，106] 范围内的件数.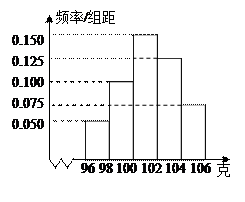
（1）若命题p为真命题，求k的取值范围；
（2）若命题p、q中恰有一个为真命题，求k的取值范围
（1）试列出两次摸球的所有可能情况；
（2）设摸到一次红、黄、白球分别记2分、1分、0分，求两次摸球总分不少于3分的概率.
（1）求椭圆C的方程；
（2）若P为椭圆C上的动点，M为过P且垂直于x轴的直线上的点，
=λ，求点M的轨迹方程