如图，在Rt△ABC中，∠C为直角，以AB上一点O为圆心，OA长为半径的圆与BC相切于点D，分别交AC、AB于点E、F．
若AC=8，AB=12，求⊙O的半径；
连接OE、ED、DF、EF．若四边形BDEF是平行四边形，试判断四边形OFDE的形状，并说明理由
（1）在如图所示的方格纸中，点P是∠AOB的边OB上的一点，不用量角器与三角尺，仅用直尺，完成下列各题：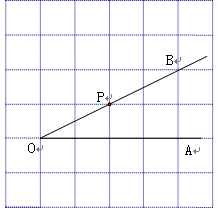
①过点P画OB的垂线，交OA于点C ；
②过点P画OA的垂线，垂足为H；
（2）在上图中线段PH的长度是点P到 的距离，线段 的长度是点C到直线OB的距离.PC、PH、OC这三条线段大小关系是 .（用“＜”号连接）
（1）化简求值：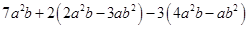
，其中
、
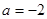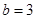
（2）已知关于x的方程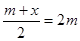
的解与方程2x-1=3的解相同，求m的值
解方程：（1）
；（2）
计算：（1）4―
－3×
；（2）
（本题12分）抛物线y=-x2+bx+c经过点A、B、C，已知A（-1，0），C（0，3）．
（1）求抛物线的解析式；
（2）如图1，P为线段BC上一点，过点P作y轴平行线，交抛物线于点D，当△BDC的面积最大时，求点P的坐标；
（3）如图2，抛物线顶点为E，EF⊥x轴于F点，M（m，0）是x轴上一动点，N是线段EF上一点，若∠MNC=90°，请指出实数m的变化范围，并说明理由．