统计中有一个非常有用的统计量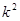，用它的大小可以确定在多大程度上可以认为“两个分类变量有关系”，下表是反映甲、乙两个平行班(甲班A老师教, 乙班B老师教)进行某学科测试，按学生考试及格与不及格统计成绩后的2×2列联表.

	不及格	及格	总计
甲班(A教)	4	36	40
乙班(B教)	16	24	40
总计	20	60	80

 
经计算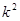＝9.6,　你认为不及格人数的多少与不同老师执教有关系的把握大约为(  　  )
下面的临界值表供参考：              

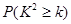	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
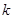	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

A．99.5%     B．99.9%    C．95%    D．无充分依据.

科目 数学   题型 选择题   难度 容易