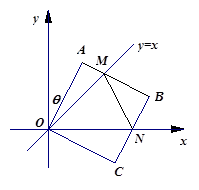
如图,在平面直角坐标中,边长为2的正方形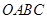 的两顶点
的两顶点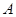 、
、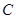 分别在
分别在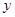 轴、
轴、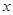 轴的正半轴上,点
轴的正半轴上,点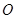 在原点.现将正方形
在原点.现将正方形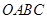 绕
绕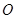 点顺时针旋转,旋转角为θ,当
点顺时针旋转,旋转角为θ,当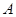 点第一次落在直线
点第一次落在直线 上时停止旋转.旋转过程中,
上时停止旋转.旋转过程中,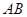 边交直线
边交直线 于点
于点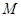 ,
,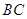 边交
边交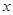 轴于点
轴于点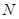 .
.
(1)当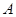 点第一次落在直线
点第一次落在直线 上时,求A、B两点坐标(直接写出结果);
上时,求A、B两点坐标(直接写出结果);
(2)设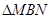 的周长为
的周长为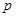 ,在旋转正方形
,在旋转正方形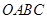 的过程中,
的过程中,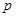 值是否有变化?请证明你的结论.
值是否有变化?请证明你的结论.
已知:如图,在 △ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
(1)求证:BC=CD;
(2)求证:∠ADE=∠ABD;
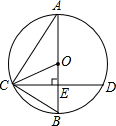
如图, 为⊙O的直径,
为⊙O的直径, 是弦,且
是弦,且

 于点E.连接
于点E.连接 、
、 、
、 。
。
(1)求证:
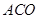 =
=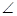
 .
.
(2)若 =18cm,
=18cm, =
=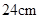 ,求⊙O的半径.
,求⊙O的半径.
透明的口袋里装有3个球,这3个球分别标有数字1、2、3,这些球除了数字以外都相同.
(1)如果从袋中任意摸出一个球,那么摸到标有数字是2的球的概率是多少?
(2)小明和小东玩摸球游戏,游戏规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小东随机摸出一个球,记下球的数字.谁摸出的球的数字大,谁获胜.现请你利用树状图或列表的方法分析游戏规则对双方是否公平?并说明理由.
如图,在直角坐标系中,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点。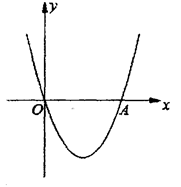
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标。
为丰富学生的学习生活,某校九年级组织学生参加春游活动,所联系的旅行社收费标准如下: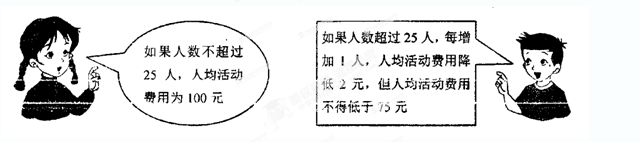
春游活动结束后,该班共支付给该旅行社活动费用2800元,请问该班共有多少人参加这次春游活动?