如图,二次函数 的图象与 轴交于点 和点 ,与 轴交于点 ,以 为边在 轴上方作正方形 ,点 是 轴上一动点,连接 ,过点 作 的垂线与 轴交于点 .
(1)求该抛物线的函数关系表达式;
(2)当点 在线段 (点 不与 、 重合)上运动至何处时,线段 的长有最大值?并求出这个最大值;
(3)在第四象限的抛物线上任取一点 ,连接 、 .请问: 的面积是否存在最大值?若存在,求出此时点 的坐标;若不存在,请说明理由.

某商店购进 、 两种商品,购买1个 商品比购买1个 商品多花10元,并且花费300元购买 商品和花费100元购买 商品的数量相等.
(1)求购买一个 商品和一个 商品各需要多少元;
(2)商店准备购买 、 两种商品共80个,若 商品的数量不少于 商品数量的4倍,并且购买 、 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
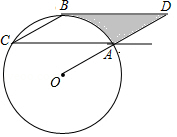
如图,点 、 、 在半径为8的 上,过点 作 ,交 延长线于点 .连接 ,且 .
(1)求证: 是 的切线;
(2)求图中阴影部分的面积.
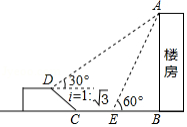
如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面 处测得楼房顶部 的仰角为 ,沿坡面向下走到坡脚 处,然后向楼房方向继续行走10米到达 处,测得楼房顶部 的仰角为 .已知坡面 米,山坡的坡度 (坡度 是指坡面的铅直高度与水平宽度的比),求楼房 高度.(结果精确到0.1米)(参考数据: ,
关于 的一元二次方程 有实数根.
(1)求 的取值范围;
(2)如果 是符合条件的最大整数,且一元二次方程 与方程 有一个相同的根,求此时 的值.