小慧和小华玩猜数游戏，小慧对小华说：“你想好一个数，这个数乘以6，加上3；得到的数除以3，再减去你想的数．只要你告诉我正确的结果，我就知道你想的数是几．”小华很好奇，就想了一个数，并按小慧说的方法计算出结果，告诉小慧说：“我计算结果是 -2．”
请你解决以下问题：
（1）小慧可以猜出小华想的数是．
（2）请你用代数方法说明，小慧为什么总能猜出别人（不一定是小华）想的数．
（3）请你也设计一个猜数游戏，要求是：让对方想一个数，按你规定的方法运算，然后你可以猜出对方的计算结果．
如
图，已知OA⊥OD，∠FOD=2∠COD，OB平分∠AOC，OE平分∠COF．
（1）若∠COD=30°，求∠BOE的度数；
（2）若∠BOE=85°，求∠COD的度数．（提示：设∠COD=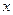
°）
一种长方形餐桌的四周可以坐6人用餐（带阴影的小长方形表示1个人的位置）．现把n张这样的餐桌按如图方式拼接起来．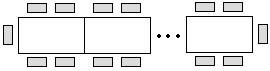
（1）问四周可以坐多少人用餐？（用n的代数式表示）
（2）若有18人用餐，至少需要多少张这样的餐桌？
如图，已知三个点A、B、C，按下列要求画图．
（1）画直线AC；
（2）连结AB；
（3）画射线BC；
（4）画线段BC的中
点D，并连结AD；
（5）画∠ACB的角平分线，交AB于E
；
（6
）过B点画直线AC的垂线，垂足为F．
（画图工具不限，不需写出结论，只需画出图形、标注字母）
先化简，再求值 
，其中
，（其中x在-2和1中任选一个）