如下图是齿轮传动装置,两个齿轮的半径比r1:r2为1:2,a、b为两轮子边缘点,c 为半径的中点,当齿轮转动时,
υa:υb:υc= ,
ωa∶ωb∶ωc= . 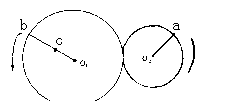
井深8m,井上支架高2m,在支架上用一根长3m的绳子系住一个重100N的物体.若以地面为参考平面,则物体的重力势能为;若以井底面为参考平面,则物体的重力势能为.
一矩形线圈面积S=10-2m2,它和匀强磁场方向之间的夹角θ1=30°,穿过线圈的磁通量Ф=1×10-3Wb,则磁场的磁感强度为______;若线圈以一条边为轴的转180°,则穿过线圈的磁能量的变化为______;若线圈平面和磁场方向之间的夹角变为θ2=0°,则Ф=______.
如图5所示, abcd是一竖直的矩形导线框,线框面积为S,放在磁场中,ab边在水平面内且与磁场方向成60°角,若导线框中的电流为I,则导线框所受的安培力对某竖直的固定轴的力矩等于______.
匀强磁场中有一段长为0.2m的直导线,它与磁场方向垂直,当通过3A的电流时,受到6.0×10-2N的磁场力,则磁场的磁感强度是______特;当导线长度缩短一半时,磁场的磁感强度是_____特;当通入的电流加倍时,磁场的磁感强度是______特.
在远距离送电时,如果输送电压为2000V,输送功率为10kW,输电线的电阻为20Ω,则输电线上损失功率为______,损失电压为______,用户得到电压为______,用户得到的功率为______.