回旋加速器的核心部分是两个半径为R的D型金属扁盒，如图，盒正中央开有一条窄缝，在两个D型盒之间加交变电压，于是在缝隙中形成交变电场，由于屏蔽作用，在D型盒内部电场很弱，D型盒装在真空容器中，整个装置放在巨大电磁铁的两极之间，磁场方向垂直于D型盒的底面，只要在缝隙中的交变电场的频率不变，便可保证粒子每次通过缝隙时总被加速，粒子的轨道半径不断增大，并逐渐靠近D型盒边缘，加速到最大能量E后，再用特殊的装置将它引出。在D型盒上半面中心出口A处有一正离子源，正离子所带电荷量为q、质量为m，加速时电极间电压大小恒为U。（加速时的加速时间很短，可忽略；正离子从离子源出发时初速为零）。则下列说法正确的是
| A．增大交变电压U，则正离子在加速器中运行时间将变短 |
| B．增大交变电压U，则正离子在加速器中运行时间将不变 |
C．正离子第n次穿过窄缝前后的速率之比为 |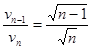
D．回旋加速器所加交变电压的频率为 |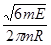
一物体做匀加速直线运动，通过一段位移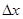
所用的时间为
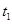，紧接着通过下一段位移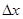所用时间为
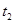。则物体运动的加速度为( )
A． |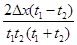
B． |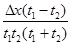
C． |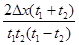
D． |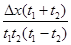
物体沿一直线运动，在t时间内通过的位移是x，它在中间位置处的速度为v1，在中间时刻的速度为v2，则v1和v2的关系不正确的是( )
| A．当物体做匀加速直线运动时，v1>v2 |
| B．当物体做匀减速直线运动时，v1>v2 |
| C．当物体做匀速直线运动时，v1=v2 |
| D．当物体做匀减速直线运动时，v1<v2 |
一质点做直线运动的位移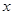
与时间
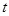的关系为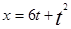
（各物理量均采用国际单位制单位），则该质点（）
| A．第1s内的位移是6m |
| B．前2s内的平均速度是6m/s |
| C．任意相邻的1s 内位移差都是1m |
| D．任意1s内的速度增量都是2m/s |
在学校科技活动组组织的“鸡蛋下落不摔破”比赛中，一同学将制作的“鸡蛋”从学校一教学楼阳台边缘由静止释放,经过一段时间到达地面,不计空气的阻力.现把“鸡蛋”在空中运动的时间分为相等的三段，如果它在第一段时间内的位移是1.25 m，那么它在第三段时间内的位移是( )
| A．1.25 m | B．3.75 m | C．6.25 m | D．10.0 m |
中国南方航空公司某架客机安全准时降落在规定跑道上，假设该客机停止运动之前在跑道上一直做匀减速直线运动，客机在跑道上滑行距离为s，从降落跑道上到停下所需时间为t，由此可知客机降落时的速度为( )
| A．s/t | B．s/2t | C．2s/t | D．条件不足，无法确定 |