如图所示，某人距离墙壁10m起跑，向着墙壁冲去，挨上墙之后立即返回出发点。设起跑的加速度为4 m/s2，运动过程中的最大速度为4 m/s，快到达墙根时需减速到零，不能与墙壁相撞。减速的加速度为8 m/s2，返回时达到最大速度后不需减速，保持最大速度冲到出发点．求该人总的往返时间为多少？
如图所示，一电荷量q=3×10-5C带正电的小球，用绝缘细线悬于竖直放置足够大的平行金属板中的O点。电键S合上后，当小球静止时，细线与竖直方向的夹角α=37°。已知两板相距d=0.1m，电源电动势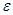
=15V，内阻r=0.5Ω，电阻R1=3Ω，R2=R3= R4 =8Ω。g取10m/s2，已知
，
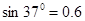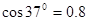。求：
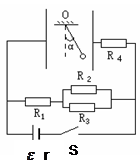17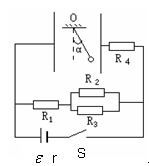
电源的输出功率；
两板间的电场强度的大小；
带电小球的质量。
如图甲所示的电路中，R1、R2均为定值电阻，且R1＝100 Ω，R2阻值未知，R3为一滑动变阻器．当其滑片P从左端滑至右端时，测得电源的路端电压随电源中流过的电流变化图线如图乙所示，其中A、B两点是滑片P在变阻器的两个不同端点得到的．求：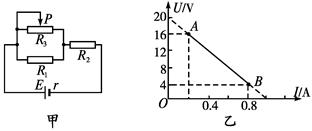
电源的电动势和内阻.
定值电阻R2的阻值．
滑动变阻器的最大阻值．
如图所示，在两根劲度系数都为k的相同的轻质弹簧下悬挂有一根导体棒ab，导体棒置于水平方向的匀强磁场中，且与磁场垂直.磁场方向垂直纸面向里，当导体棒中通以自左向右的恒定电流时，两弹簧各伸长了Δl1；若只将电流反向而保持其他条件不变，则两弹簧各伸长了Δl2，求：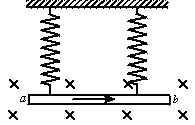
导体棒通电后受到的磁场力的大小?
若导体棒中无电流，则每根弹簧的伸长量为多少?
如图所示，电源电动势E＝6V，电源内阻不计．定值电阻R1=2.4kΩ、R2="4.8kΩ." 若在ab之间接一个C=100μF的电容器，闭合开关S，电路稳定后，求电容器上所带的电量；
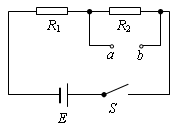
若在ab之间接一个内阻RV = 4.8kΩ的电压表，求电压表的示数．
如图所示，匀强电场区域和匀强磁场区域是紧邻的且宽度相等均为d，电场方向在纸平面内，而磁场方向垂直纸面向里．一带正电粒子从O点以速度v0沿垂直电场方向进入电场．在电场力的作用下发生偏转，从A点离开电场进入磁场，离开电场时带电粒子在电场方向的偏移量为d，当粒子从C点穿出磁场时速度方向与进入电场O点时的速度方向一致，不计带电粒子的重力，求：
粒子从C点穿出磁场时的速度v.
电场强度和磁感应强度的比值.