如图,在平面直角坐标系中,点C(-3,0),点A、B分别在x轴,y轴的正半轴上,且满足 .
.求点A、B坐标
若点P从点C出发,以每秒1个单位的速度沿射线CB运动,连接AP。设△ABP面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围
在(2)的条件下,是否存在点P,使以点A、B、P为顶点的三角形与△AOB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由。

解不等式组: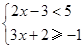
某“希望学校”为加强信息技术课教学,拟投资建一个初级计算机房和一个高级计算机房,每个机房只配置1台教师用机,若干台学生用机.现有厂方提供的产品推介单一份,如下表.
产品推介单
| 类别 |
初级机房 |
高级机房 |
| 机型 |
 型 型 |
 型 型 |
 型 型 |
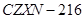 型 型 |
|
| 生产 日期 |
2005年1月 |
2005年3月 |
| 单 价 |
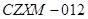 型 型10000元 |
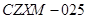 型 型14375元 |
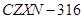 型 型4375元 |
 型 型8750元 |
|
| 性能 |
多人交互 |
 |
 |
 |
 |
现知:教师配置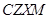 系列机型,学生配置
系列机型,学生配置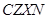 系列机型;所有机型均按八折优惠销售,两个机房购买计算机的钱数相等,并且每个机房购买计算机的钱数不少于20万元也不超过21万元.
系列机型;所有机型均按八折优惠销售,两个机房购买计算机的钱数相等,并且每个机房购买计算机的钱数不少于20万元也不超过21万元.
请计算,拟建的两个机房各能配置多少台学生用机?
解不等式组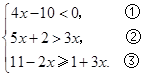
为美化青岛,创建文明城市,园林部门决定利用现有的3600盆甲种花卉和2900盆乙种花卉搭配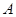 、
、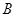 两种园艺造型共50个,摆放在迎宾大道两侧.搭配每个造型所需花卉情况如右表所示:
两种园艺造型共50个,摆放在迎宾大道两侧.搭配每个造型所需花卉情况如右表所示: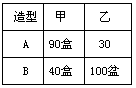
结合上述信息,解答下列问题:
(1)符合题意的搭配方案有哪几种?
(2)若搭配一个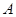 种造型的成本为1000元,搭配一个
种造型的成本为1000元,搭配一个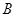 种造型的成本为1200元,试说明选用(1)中哪种方案成本最低?
种造型的成本为1200元,试说明选用(1)中哪种方案成本最低?
南宁市是广西最大的罗非鱼养殖产区,被国家农业部列为罗非鱼养殖优势区域.某养殖场计划下半年养殖无公害标准化罗非鱼和草鱼,要求这两个品种总产量 (吨)满足:
(吨)满足: ,总产值为1000万元.已知相关数据如右表所示.
,总产值为1000万元.已知相关数据如右表所示.
| 品种 |
单价(万元/吨) |
| 罗非鱼 |
0.45 |
| 草鱼 |
0.85 |
求:该养殖场下半年罗非鱼的产量应控制在什么范围?(产值=产量 单价)
单价)