在有理数范围内,下列各多项式能用公式法进行因式分解的是( )。
| A.a2-6a | B.a2-ab+b2 | C.a2-ab+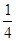 b2 b2 |
D.a2-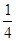 ab+b2 ab+b2 |
学校为了解七年级学生参加课外兴趣 小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( ▲ )
小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( ▲ )
| A.0.1 | B.0.15 |
| C.0.25 | D.0.3 |

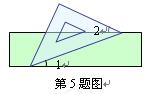
如图,把一块含有 45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20o,那么∠2的度数是( ▲ )
45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20o,那么∠2的度数是( ▲ )
| A.30o | B.25o |
| C.20o | D.15o |
有四包真空小包装火腿,每包以标准克数(450克)为基准,超过的克数记作正数,不足的克数记作负数,以下数据是记录结果,其中表示实际克数最接近标准克数的是( ▲ )
| A.+2 | B. 3 3 |
| C.+3 | D.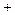 4 4 |
下列各式能用完全平方公式进行分解因式的是( ▲ )
| A.x2+1 | B.x2+2x-1 | C.x2+x+1 | D.x2+4x+4 |
如图是六个棱长为1的立方块组成的一个几何体,其俯视图的面积是( ▲ )
| A.6 | B.5 | C.4 | D.3 |
